ALÉA 2019
Introduction à l'algorithmique du texte
Julien Clément (GREYC, Caen)
Remerciements à Véronique Terrier pour les emprunts et son aide
Quelques liens utiles
Introduction

Rechercher un motif dans un texte, indexer des données textuelles, expliciter les régularités d'un texte sont des problèmes omniprésents en informatique
→
éditeur de texte, moteur de recherche, bases de données textuelles, analyse de séquences biologiques, compression
Contingences pratiques :
- on travaille sur des données de grande taille
→ il est impératif de trouver des algorithmes qui soient de petites complexités à la fois en temps et en espace - les données sont des séquences de caractères et n'ont pas de structure explicite
→ définir des algorithmes rapides nécessite de définir les structures adéquates pour représenter et manipuler efficacement les chaînes de caractères (structures pas trop coûteuses à construire et peu gourmandes en espace)
D'ailleurs, qu'est-ce qu'un texte ?
D'ailleurs, qu'est-ce qu'un texte ?
Exemples



- Homo_sapiens.GRCh38.dna.chromosome.1 (225 080 Ko, ASCII)
- L'assommoir (Emile Zola, 930Ko, latin1)
Gervaise avait attendu Lantier jusqu'à deux heures du matin. Puis, toute frissonnante d'être restée en camisole à l'air vif de la fenêtre, elle s'était assoupie, jetée en travers du lit, fiévreuse, les joues trempées de larmes. Depuis huit jours, au sortir du Veau à deux têtes, où ils mangeaient, il l'envoyait se coucher avec les enfants et ne reparaissait que tard dans la nuit, en racontant qu'il cherchait du travail. Ce soir-là, pendant...
- War and Peace (Léon Tolstoï, 3110 Ko, ASCII)
Well, Prince, so Genoa and Lucca are now just family estates of the Buonapartes. But I warn you, if you don't tell me that this means war, if you still try to defend the infamies and horrors perpetrated by that Antichrist--I really believe he is Antichrist--I will have nothing more to do with you and you are no longer my friend, no longer my 'faithful slave,' as you call yourself! But how do you do? I see I have frightened you--sit down and tell me all the news." It was...
D'ailleurs, qu'est-ce qu'un texte ?
L'encodage : un détail important !
UTF-8
- code à longueur variable (1 à 4 octets)
- pouvant représenter le standard UNICODE (1 112 064 symboles)
- rétro-compatible avec ASCII
Depuis : 87,6 % en 2016, 90,5 % en 2017 et près de 93.1% en février 2019
(usage pour le web - sources : wikipedia)
Recherche de motifs
Partie 1
Notations
- Un alphabet $\Sigma$ : un ensemble fini de symboles, appelés lettres ou caractères
- Un mot ou un texte sur l'alphabet $\Sigma$ : une suite de lettres de $\Sigma$
- La longueur d'un mot w, notée $|w|$ : le nombre de lettres du mot
- Le mot vide, i.e., le mot de longueur $0$ : $\varepsilon$
- Par convention, on indice les lettres d'un mot à partir de $0$ :
$w=w[0]w[1]\dots w[n-1]$ avec $n=|w|$
- La séquence de lettres partant de la position $i$ et de longueur $j$ :
$w[i..i+j-1]=w[i] w[i+1]\dots w[i+j-1]$
- $\Sigma^*$ : l'ensemble de tous les mots sur $\Sigma$
- $\Sigma^+$ : l'ensemble de tous les mots non vides sur $\Sigma$
Notations (suite)
- Les préfixes de $w$ : \[ \text{Pref}(w) = \{ \textcolor{red}{x} : \text{ il existe $y \in \Sigma ^*$ tel que $w= \textcolor{red}{x}y$}\}\]
- Les suffixes de $w$ : \[\text{Suf}(w) = \{ \textcolor{red}{y} : \text{ il existe $x \in \Sigma ^*$ tel que $w= x\textcolor{red}{y}$}\}\]
- Les facteurs de $w$ : \[ \text{Fact}(w) = \{ \textcolor{red}{z} : \text{ il existe $x , y \in \Sigma ^*$ tel que $w= x\textcolor{red}{z}y$}\}\]
Un préfixe, suffixe ou facteur d'un mot $w$ est propre, s'il est différent de $w$ lui-même.
Soit $w = abbaac$, on a
- $\text{Pref}(w)=\{\varepsilon,a,ab,abb,abba,abbaa,abbaac\}$
- $\text{Suf}(w)=\{\varepsilon,c,ac,aac,baac,bbaac,abbaac\}$
- $\text{Fact}(w)=\{\varepsilon,\,a,b,c,\,aa,ab,ac,ba,bb,\, aac,abb,baa,bba,abba,$
$baac,bbaa,abbaa,bbaac,abbaac\}$
Différentes notions et approches pour la recherche de motif
(Pattern matching)
- Motif vu comme
- un mot (fini)
- une expression régulière
- un ensemble fini de mots
- un mot approché
- Techniques variées
- stratégie de la fenêtre coulissante
- basées sur les automates finis
- avec une structure d'arbre (Trie, arbre de suffixes)
- via de la programmation dynamique
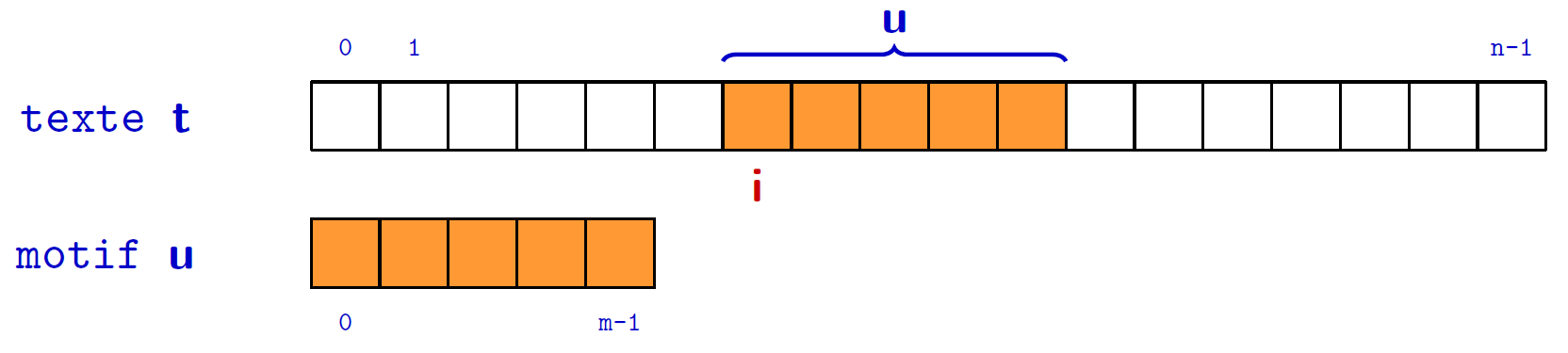
Recherche de motif
Trouver les occurrences d'un motif $u\in \Sigma^+$ dans un texte $t\in \Sigma^+$
Deux types de solutions
- Motif fixé, texte variable
- Prétraitement sur le motif basé sur des propriétés combinatoires du motif
- Recherche
- Texte fixé, motif variable
- Prétraitement sur le texte basé sur des techniques d'indexation
- Recherche
Quel type d'occurrences? chevauchantes ? non-chevauchantes ?
Je n'aborde pas ici les techniques classiques de théorie des automates
Stratégie de la fenêtre coulissante
Balayage et Décalage (Scan & Shift)
On lit le texte au travers d'une fenêtre coulissante de la taille du mot.
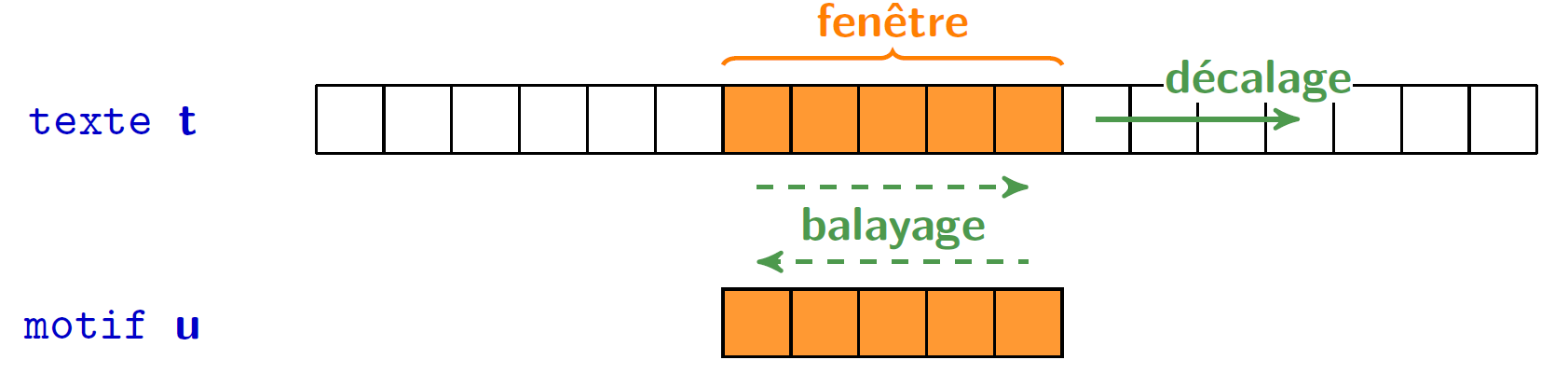
Schéma de base
Positionner la fenêtre au début du texte
Tant que la fenêtre est sur le texte
Si fenêtre == motif alors /* Balayage */
Signaler occurrence
Décaler la fenêtre /* Décalage */Algorithme naïf
Recherche exhaustive
- Avec un balayage de gauche à droite
- Avec un shift systématique de +1 sur le texte
def naive_search(u, t):
m = len(u)
n = len(t)
i = 0
j = 0
while i < n-m+1:
while j < m and u[j] == t[i+j]: # scan
j = j+1
if j == m:
signal_occurrence(i) # signaler une occurrence à la position i
i = i+1 # shift
j = 0
Algorithme naïf
Exemple
- Le texte : $t=aababbabababb$ ($\lvert t \rvert = 13$)
- Le motif cherché : $u=ababa$
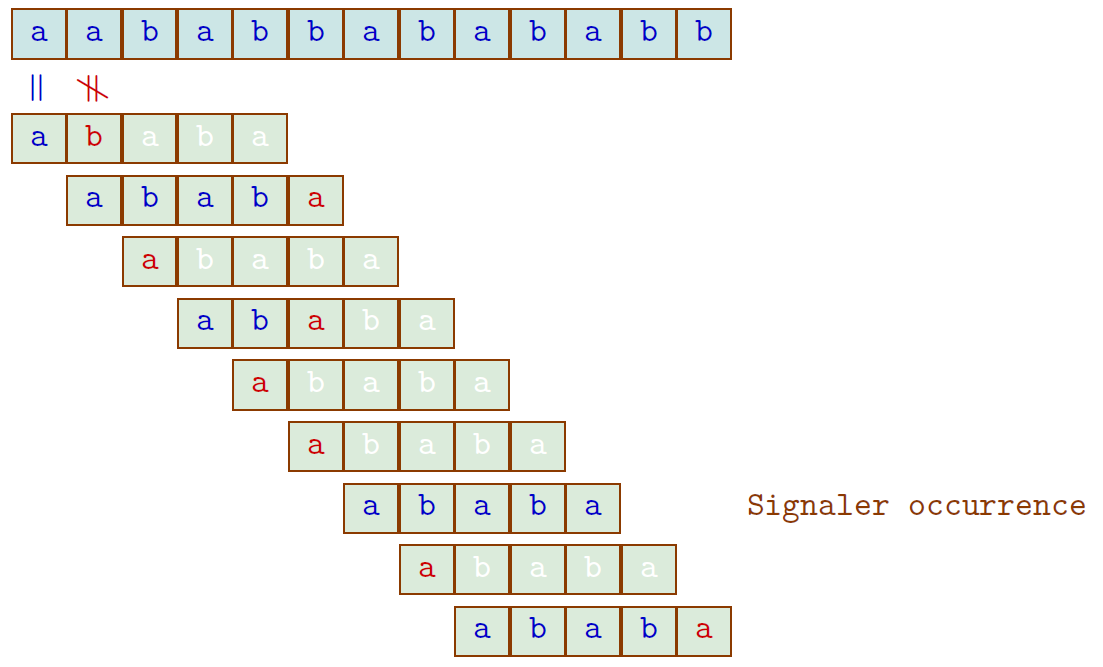
→ $24$ comparaisons
Algorithme naïf
Coût de l'algorithme au pire
Quel est le nombre maximal de comparaisons de l'algorithme naïf avec un texte de longueur $n$ et un motif de longueur $m$ ?
$(n-m+1)\times m$, i.e., une complexité au pire en $\color{red}O(nm)$ → quadratique !
Exemple
ce nombre maximal est atteint pour $t=a^n$ , $u=a^m$Coût moyen de l'algorithme
- $\sigma\ge 2$ dénote le nombre de lettres de l'alphabet $\Sigma$
- On se place dans le cas simple où toutes les lettres du texte et du mot sont tirées indépendamment avec une probabilité uniforme.
- Nombre moyen de comparaisons réalisées : \begin{align*} %\sum\limits_{k=1}^m k(\frac{1}{\sigma^{k-1}}-\frac{1}{\sigma^k})\,+\frac{m}{\sigma^m} %&=\sum\limits_{k=1}^m\frac{1}{\sigma^{k-1}} + \sum\limits_{k=1}^m(\frac{k-1}{\sigma^{k-1}}-\frac{k}{\sigma^k})+\frac{m}{\sigma^m}\\ %&=\sum\limits_{k=0}^{m-1}\frac{1}{\sigma^k}= n \frac{1-1/\sigma^m}{1-1/\sigma}&\leq\frac{1}{1-1/\sigma} \leq 2n \end{align*}
Le coût moyen est linéaire en la taille du texte, i.e., en $O(n)$
Algorithme naïf $\rightarrow$ Algorithme de Morris-Pratt
- Algo naïf : on oublie tout à chaque décalage
- Algo de Morris-Pratt : on mémorise les caractères du mot appareillés à ceux du texte
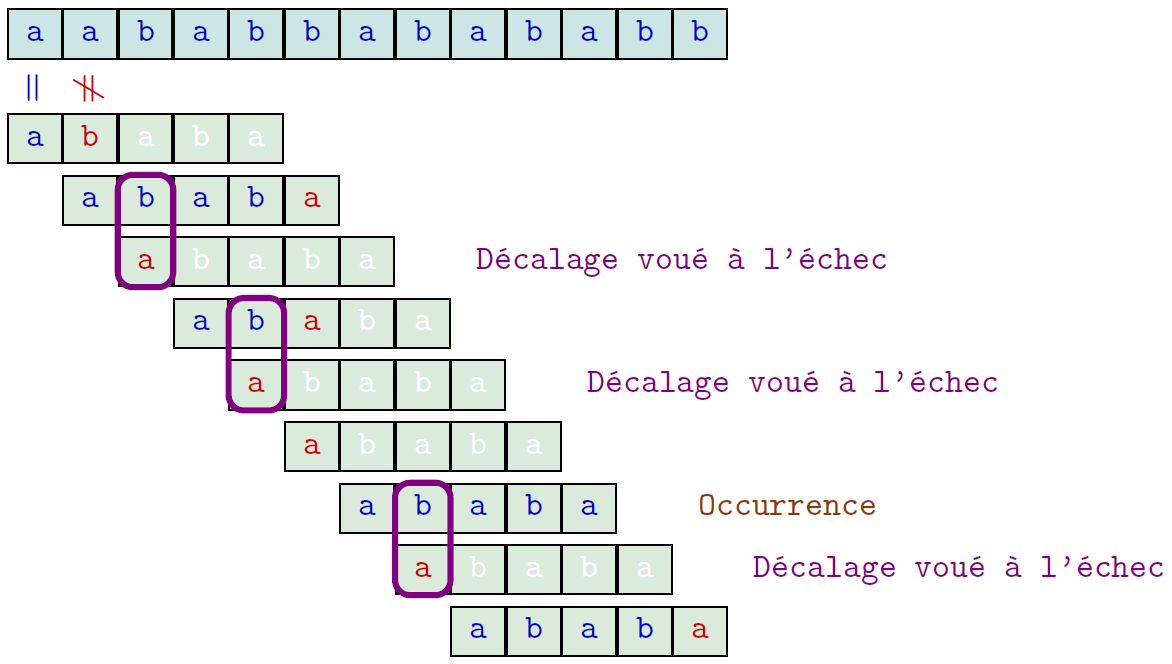
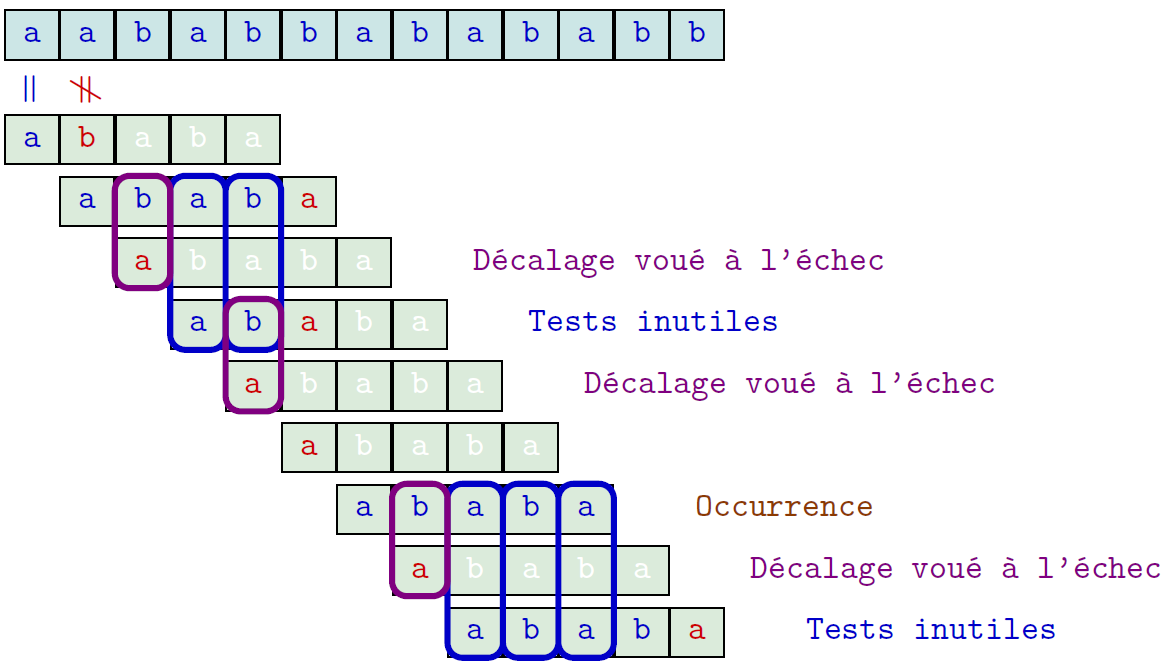
Algorithme naïf $\rightarrow$ Algorithme de Morris-Pratt
Principe
- Le balayage se fait de gauche à droite.
- Le décalage de la fenêtre est calculé à partir du motif et de ses bords
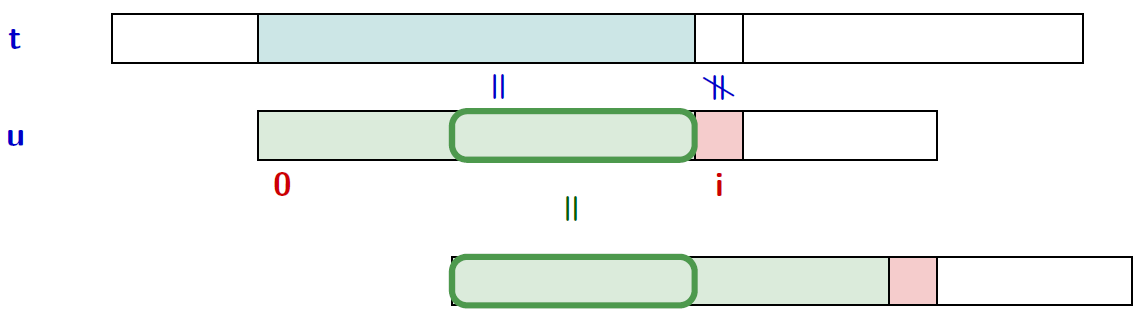
Calculer un "bon" décalage suite à un échec à la position $i$ :
- Déterminer un préfixe propre de $u[0..i-1]$ qui soit également suffixe de $u[0..i-1]$,
- on veut le plus grand.
→ notion de bord
Bord
- Un bord d'un mot $w$ est un mot différent de $w$ qui est à la fois préfixe et suffixe de $w$
- Le bord maximal de $w$, noté $\text{Bord}(w)$, est le plus long bord de $w$
- $w = abaababa$ :
- ensemble des bords de $w$ : $\{\varepsilon,a,aba\}$
- $\text{Bord}(w) = aba$
- $w = aabaabaa$
- ensemble des bords de $w$ : $\{\varepsilon,a,aa,aabaa\}$
- $\text{Bord}(w) = aabaa$
Calculer le Bord
Pour tout mot $u\in \Sigma^+$ et tout caractère $a\in \Sigma$ :
\[ \text{Bord}(ua)= \begin{cases} \text{Bord}(u)a &\text{si $\text{Bord}(u)a$ est un préfixe de $u$}\\ \text{Bord}(\text{Bord}(u)a)&\text{sinon} \end{cases} \]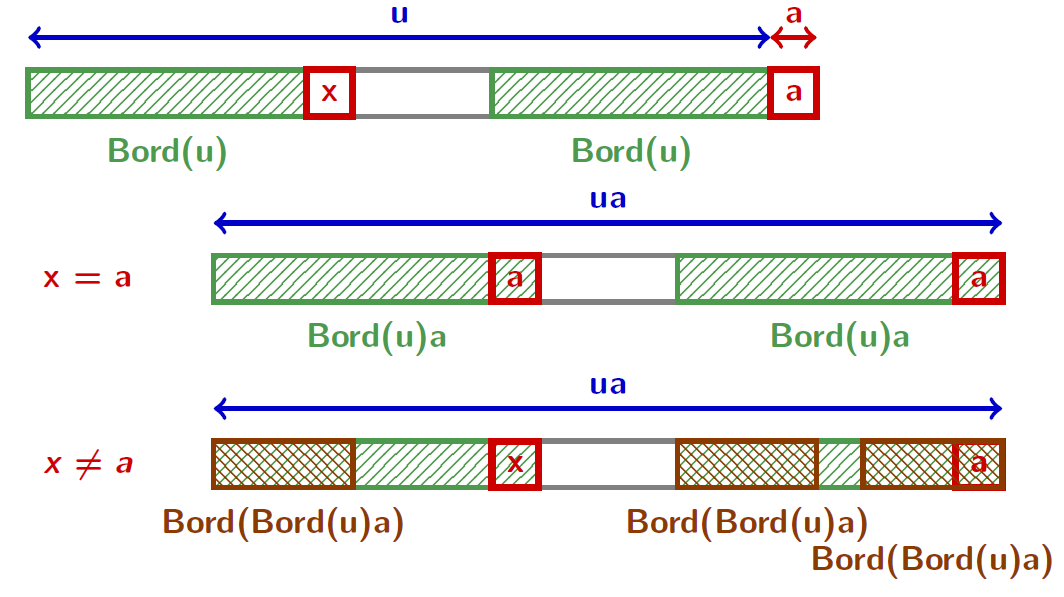
La table des bords
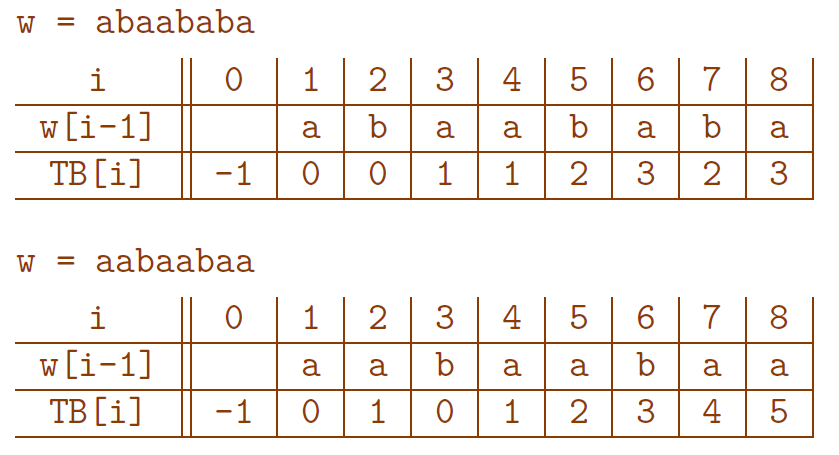
Calculer la table des bords
L'algorithme
def Bord(u):
m = len(u)
TB = [0 for i in range(m+1)]
j = -1
for i in range(0,m):
TB[i] = j
while(j >= 0 and u[j] != u[i]):
j = TB[j]
j = j+1
TB[m] = j
return TB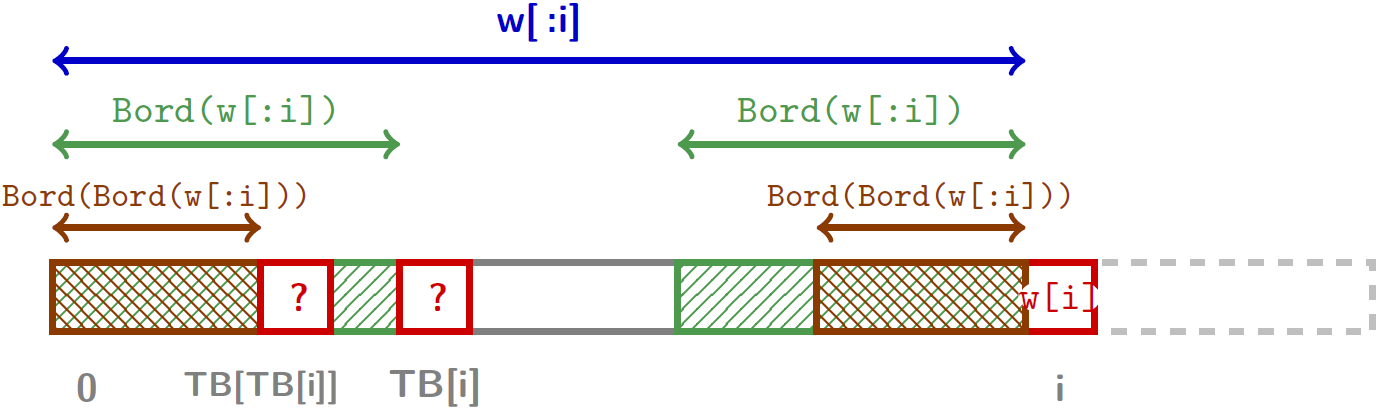
Calculer la table des bords
Complexité de l'algorithme
La complexité au pire est linéaire en la taille $m$ du mot
Complexité est linéaire en le nombre de comparaisons entre lettres
$\approx$ Nombre total de fois où la condition du while est examinée
def Bord(u):
m = len(u)
TB = [0 for i in range(m+1)]
j = -1
for i in range(0,m):
TB[i] = j
while(j >= 0 and u[j] != u[i]): # comparaisons effectuées ici !!!
j = B[j]
j = j+1
TB[m] = j
return TB(Preuve typique) La quantité $\Delta(i, j) = 2i-j$ augmente au moins de 1 à chaque comparaison
- Au début : $\Delta(0, -1) = 1$
- À la fin : $\Delta(m-1, j) \le 2m-2$.
Algorithme de Morris-Pratt
- Le texte et le motif cherché : $t=aababbabababb$ et $u = ababa$
- Table des bords de $u$
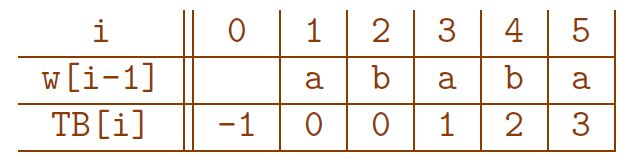
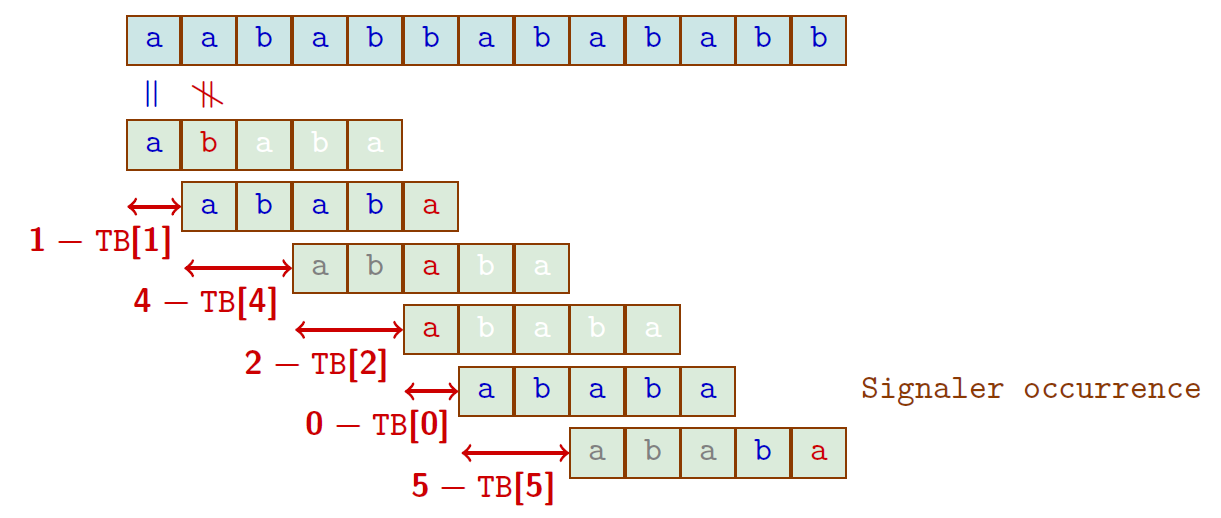
$16$ comparaisons
(À chaque étape, il est inutile de tester les $B[i]$ premiers caractères du motif; $TB[0] =-1$ permet de toujours décaler au moins de 1)
Recherche de motif
Utilisation de la table des bords
def findMP(u, t, TB=None):
m = len(u)
n = len(t)
if TB is None:
TB = Bord(u)
i, j = 0, 0
while i < n-m+1:
while j < m and u[j] == t[i+j]:
j = j+1
if j == m:
signal_occurrence(i)
i = i + j - TB[j] # décalage calculé avec la table des bords
if j != 0:
j = TB[j] # pas la peine de comparer les symboles déjà appareillés
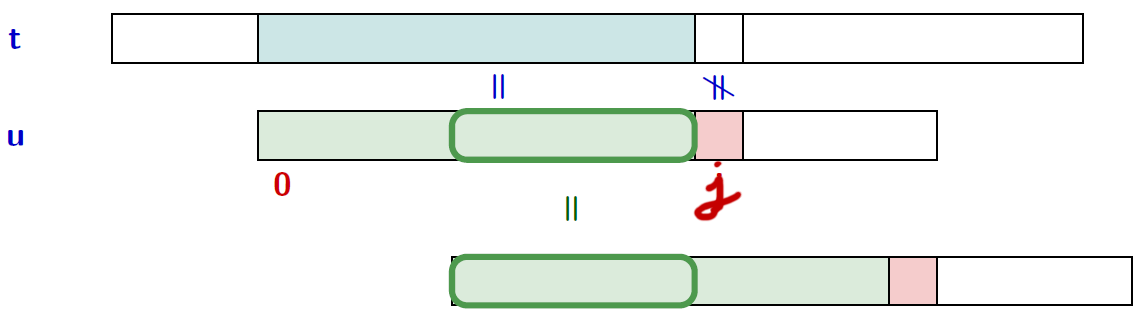
→ Décalage : j-TB[j]
Algorithme de Morris-Pratt
Complexité de l'algorithme
La complexité au pire est linéaire en $m+n$, somme des tailles du mot et du texte
- coût du prétraitement sur le motif :
Le calcul de la table des bords a un coût en $O(m)$ - coût de la recherche : $O(n)$
Considérer la quantité $\Delta'(2i+j)$
(croît au moins de 1 à chaque comparaison)
De Morris-Pratt à Knuth-Morris-Pratt
- MP : on mémorise les caractères du mot appareillés à ceux du texte
- KMP : on mémorise aussi les erreurs (un peu !)
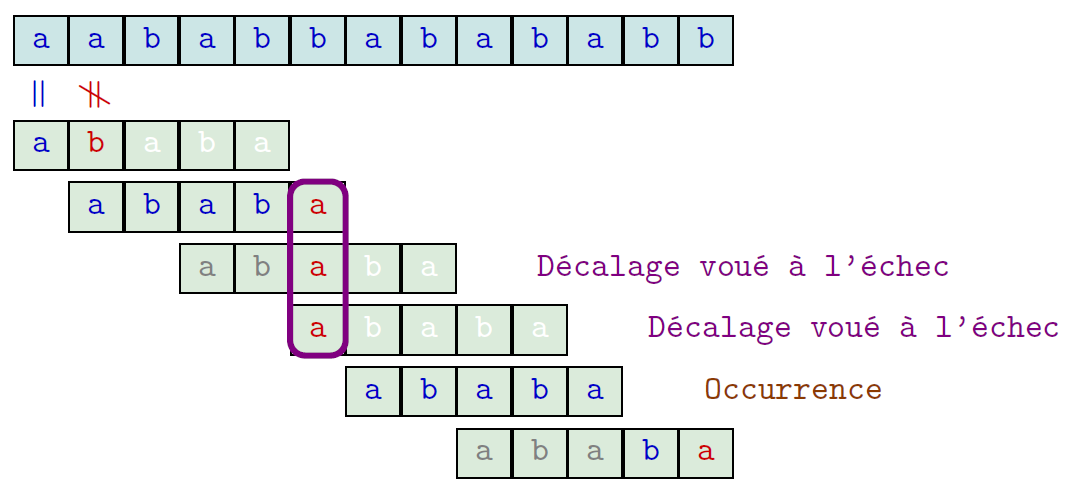
De Morris-Pratt à Knuth-Morris-Pratt
Knuth-Morris-Pratt
- Le balayage se fait de gauche à droite.
- Le décalage de la fenêtre est calculé à partir du motif et de ses bords stricts
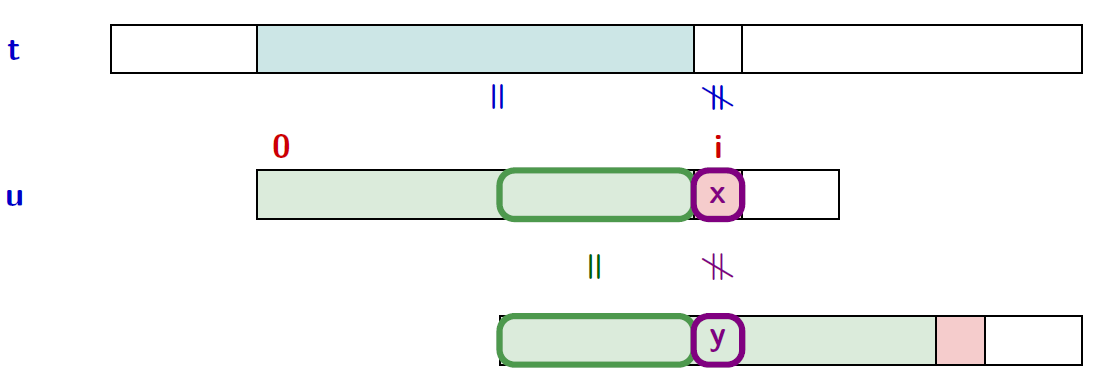
Calculer un « bon » décalage suite à un échec à la position $i$ :
- Déterminer un préfixe propre de $u[0..i-1]$ qui soit suffixe de $u[0..i-1]$,
- tel que le caractère $y$ suivant ce préfixe est différent du caractère $x$ suivant le suffixe (i.e., le caractère qui a provoqué l'échec)
- on veut le plus grand
→ notion de bord strict
Bord strict
Définition
Soit $w$ un mot et $v$ un préfixe de $w$. $b$ est un bord strict de $v$ relativement à $w$ si- $b$ est un bord de $v$
- $v = w$ ou $w[|v|] \neq w[|b|]$
« Le bord strict maximal » de $v$ (relativement à $w$), noté $\text{BordStrict}(v, u)$, est le plus long bord strict de $v$ quand il existe.
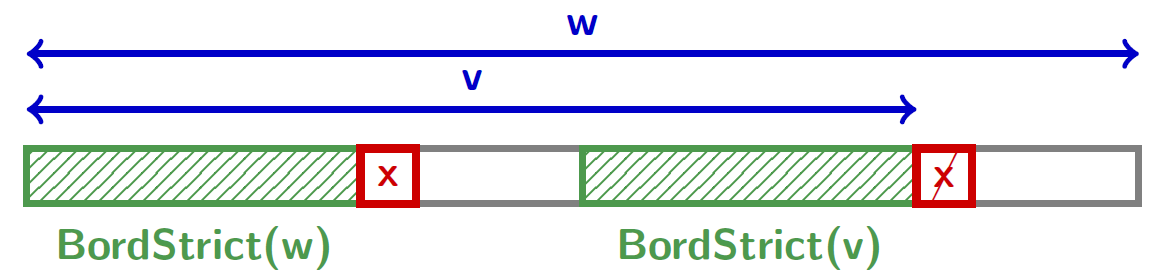
Remarque : Le bord strict n'est pas toujours défini.
Par exemple, le préfixe $ab$ n'admet pas de bord strict relativement à $aba$
La table des bords stricts
On calcule facilement la table des bords stricts à partir de celle des bords \[ SB[0]= -1, \qquad SB[|w|]= TB[|w|], \] et pour $0\lt i \lt |w|$, on a \[ SB[i]= \begin{cases} TB[i]&\text{si $w[i]\neq w[TB[i]]$}\\ SB[TB[i]]&\text{sinon} \end{cases} \]
La table des bords stricts
Exemple
$w = ababa$
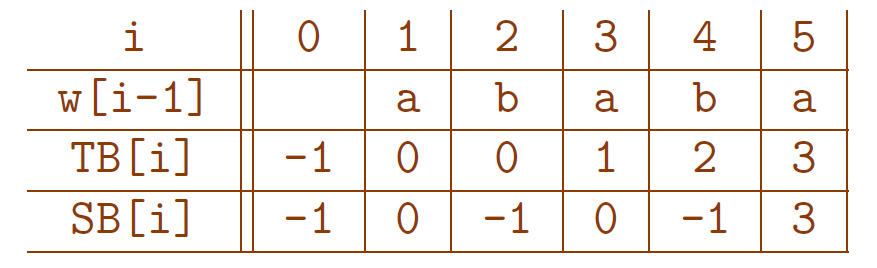
- Représentation de $TB$
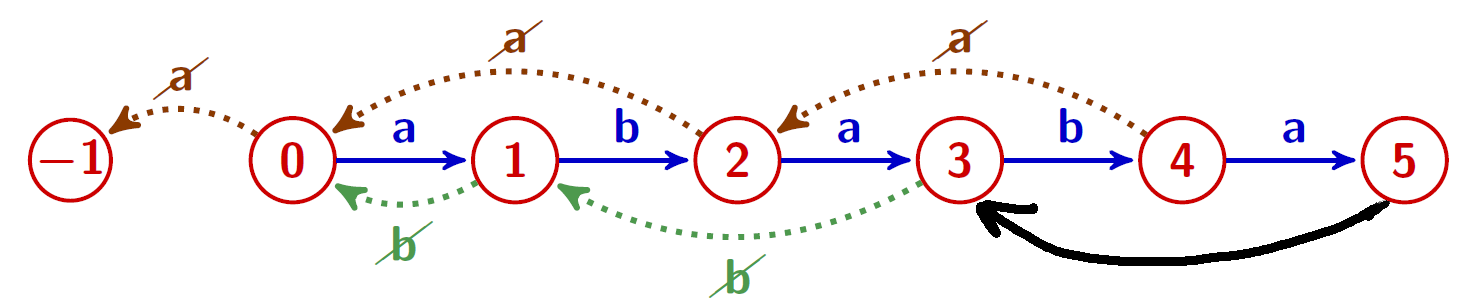
- Représentation de $SB$
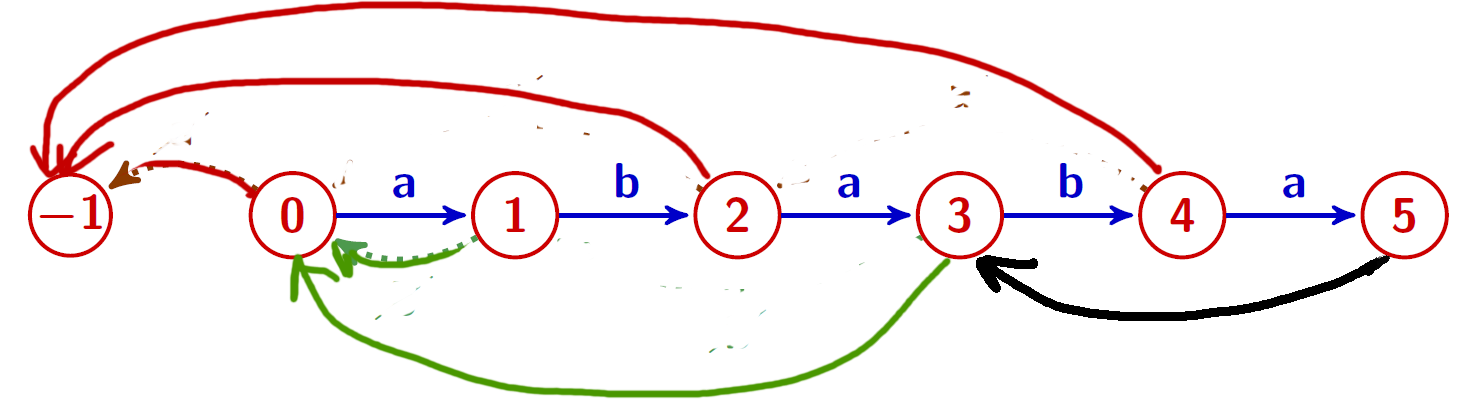
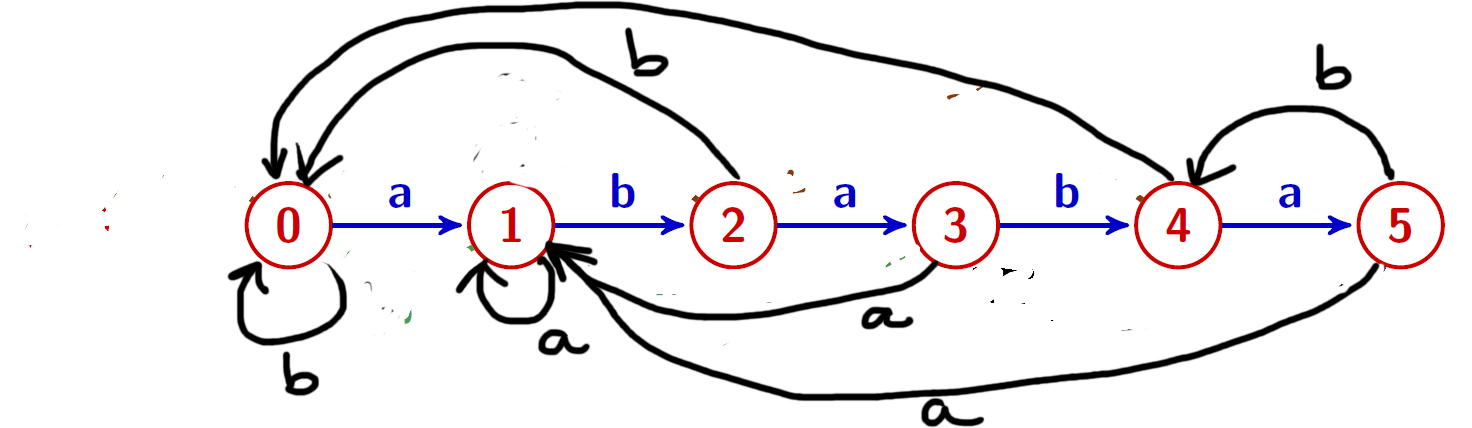 (Préparation pour l'automate d'Aho-Corasick...)
(Préparation pour l'automate d'Aho-Corasick...)Morris-Pratt et Knuth-Morris-Pratt
Entrée : Un mot \$u$ de longueur $m$ et un texte $t$ de longueur $n$
- Prétraitement
- calcul de la table des bords $O(m)$
- calcul de la table des bords stricts $O(m)$
- Recherche $O(n)$ pour Morris-Pratt et Knuth-Morris-Pratt
même algo hormis le décalage calculé avec les bords stricts :
i = i+j-TB[j]→i = i+j-SB[j]
Mais alors ?
- $m$ pour MP
- $\log_{\phi}(1+m)$ où $\phi=\frac{1+\sqrt{5}}{2}$pour KMP
Utile si on veut un algo à faible délai entre deux caractères traités (applications temps réel)
Knuth-Morris-Pratt
Exemple
$u = ababa$, $t=aababbabababb$MP
16 comparaisons
KMP
14 comparaisons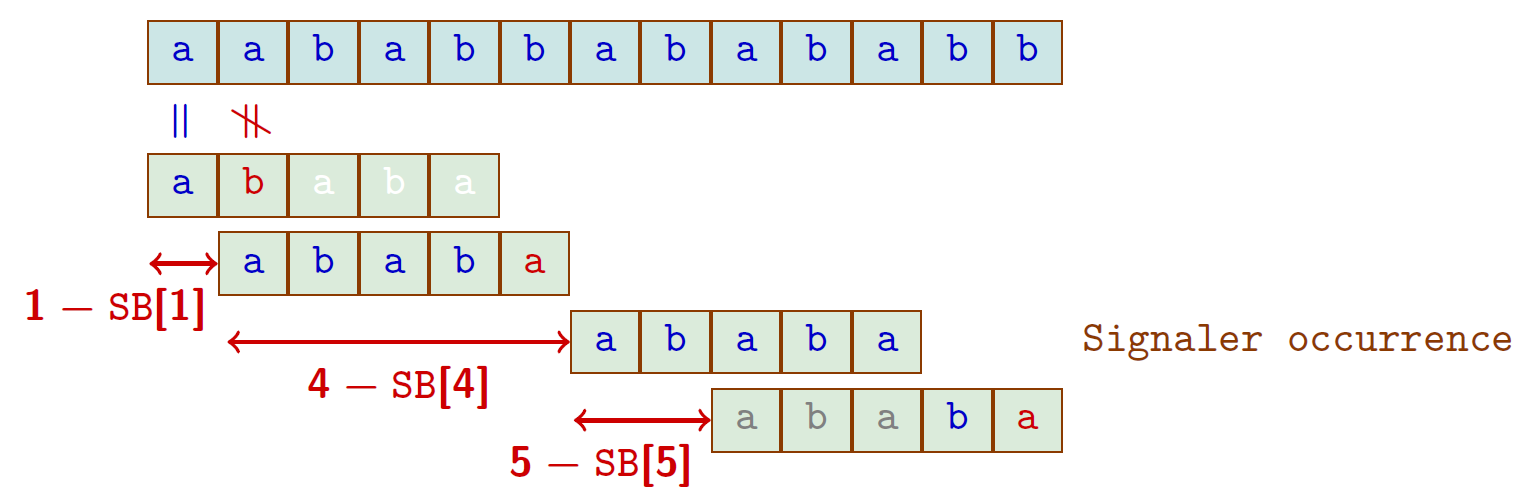
Toute une zoologie d'algorithmes
Un autre exemple : algorithme du facteur miroir
Recherche : On applique l'automate qui reconnaît les suffixes du miroir sur les lettres de la fenêtre lue de droite à gauche
- À chaque fois que l'automate entre dans un état d'acceptation (sans que toutes les lettres de la fenêtre n'aient été consommées) on mémorise sa position. Cette position correspond à celle du plus grand suffixe du miroir jusqu'à présent rencontré.
- Lorsque l'automate s'arrête, soit parce qu'il se bloque (cas d'échec) ou que toutes les lettres de la fenêtre ont été consommées (occurrence détectée), la position précédemment mémorisée spécifie alors le décalage à effectuer.
Toute une zoologie d'algorithmes
algorithme du facteur miroir
$u=bababb$
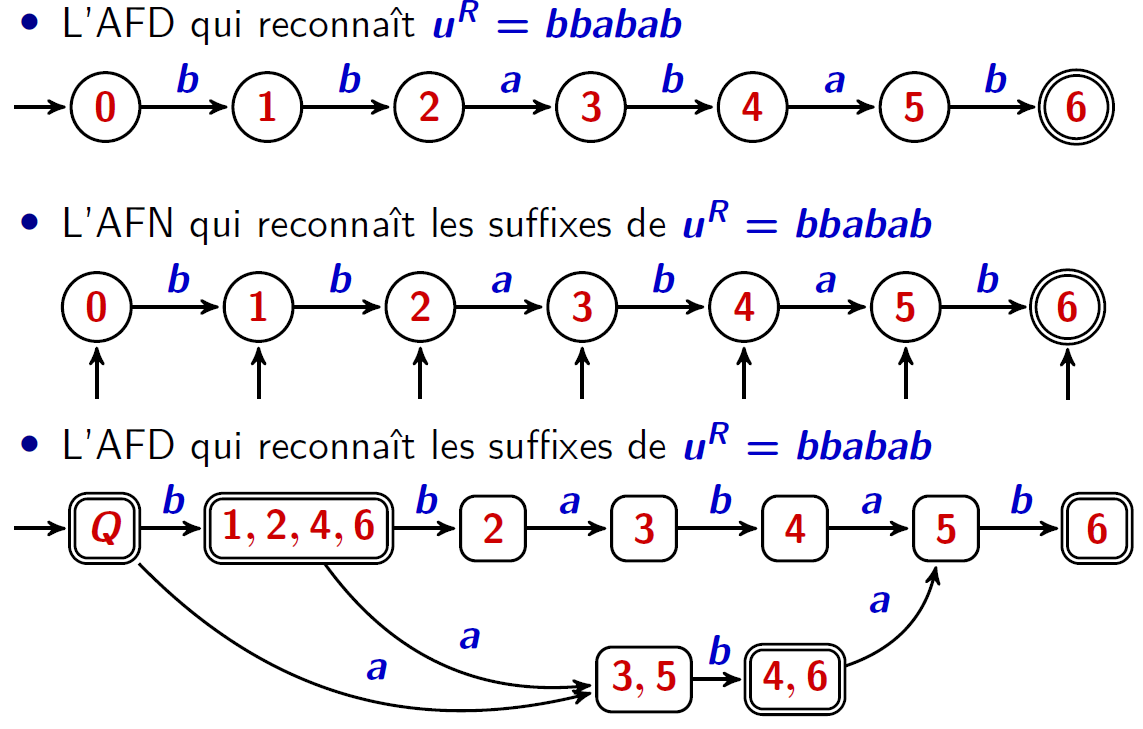
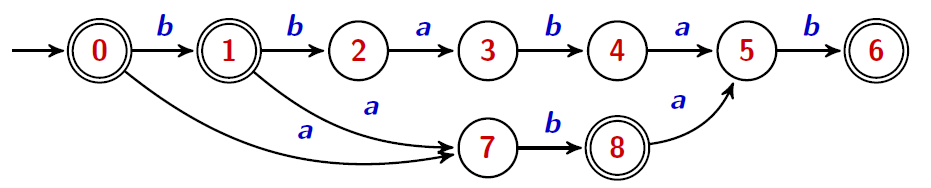



Toute une zoologie d'algorithmes
Boyer-Moore
Principe
- La lecture se fait de droite à gauche.
- Le décalage de la fenêtre est calculé suivant deux règles :
- la règle du bon caractère (heuristique simple)
- la règle du bon suffixe (utilise deux tables)
Dans le pire des cas : l'algorithme original e complexité en temps en $O(nm)$ si le motif est présent, $O(n+m)$ si le motif n'est pas présent
Très efficace en pratique (et compatible avec le codage UTF-8)
Toute une zoologie d'algorithmes
Boyer-Moore : Règle du bon caractère
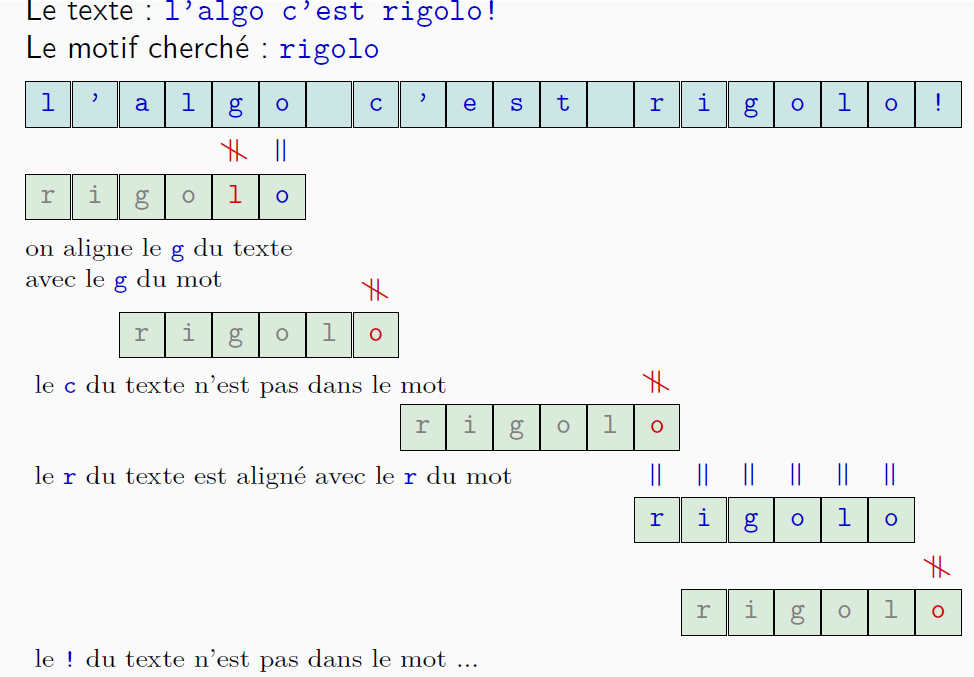
Cela fonctionne «bien» (sous-linéaire) lorsque l'alphabet est grand
Aho Corasick
Un cas important : le motif recherché est un ensemble (fini) de mots (finis)
On peut toujours effectuer la recherche un à un de chaque mot de l'ensemble mais ça ne va pas être efficace.
Problème
Étant donné un texte $t$ et un ensemble $X=\{u_1,\dots,u_k\}$ de $k$ mots, trouver toutes les occurrences de $u_1,\dots,u_k$ dans $t$.Si l'on note $m=|u_1|+\dots+|u_k|$ la taille de l'ensemble $X$ et $n$ la taille du texte, on souhaiterait des algorithmes linéaires en $m+n$
Aho Corasick
Arbre lexicographique (trie développé)
Une structure de donnée adéquate pour représenter un ensemble de mots
- les arêtes sont étiquetées par des caractères
- toutes les arêtes issues d'un même nœud ont des étiquettes distinctes.
À chaque nœud de l'arbre correspond le mot formé des caractères qui étiquettent le chemin de la racine à ce nœud.
Les feuilles et certains nœuds internes sont marqués, ils représentent les mots de l'ensemble.
→ plus exactement variante qui sépare les mots exactement selon les préfixes
Aho Corasick
Arbre lexicographique (trie développé)
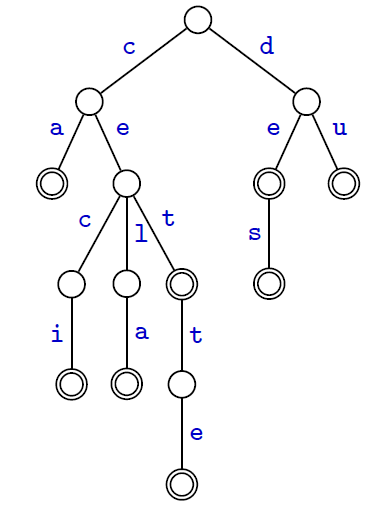
- L'arbre représente l'ensemble
$X=${ca, ceci, cela, ces, cet, cette, de, des, du} - L'ensemble des nœuds de l'arbre code les préfixes des mots de $X$ :
$\text{Pref}(X)=${$\varepsilon$, c, d, ca, ce, de, du, cec, cel, cet, des, ceci, cela, cett, cette}
Aho Corasick
L'automate arbre qui reconnaît $\Sigma^*X$
Ses caractéristiques :- $X = \{ab, bab, babb, bb\}$
- ses états correspondent aux nœuds de l'arbre lexicographique :
$\text{Pref}(X)=\{\varepsilon,a,b,ab,ba,bb,bab,babb\}$ - son état initial est la racine : $\varepsilon$
- ses états d'acceptations : $\text{Pref}(X)\cap\Sigma^*X = \{ab,bb,bab,babb\}$
- sa fonction de transition :
$\delta(p,x)= \begin{cases} px&\text{si $px\in \text{Pref}(X)$}\\ \text{le plus long suffixe propre de $px \in \text{Pref}(X)$}&\text{sinon} \end{cases}$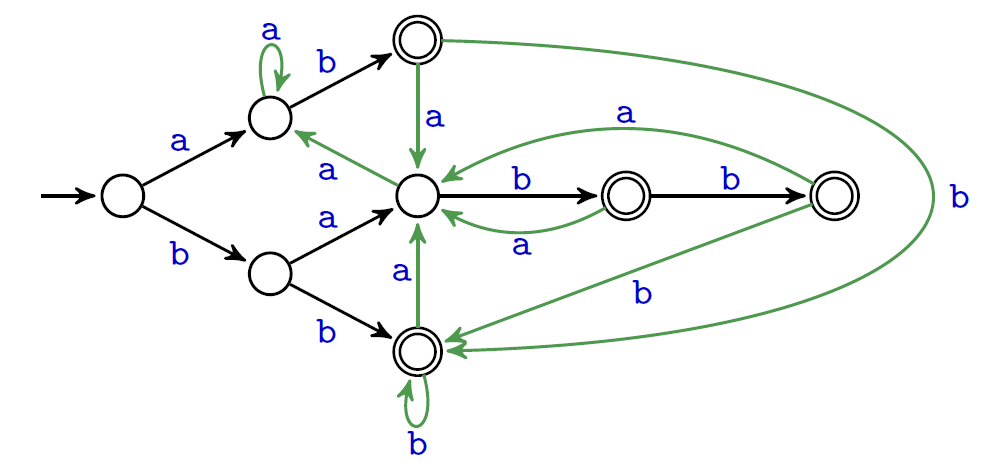
Problème : L'automate est complet → beaucoup de transitions inutiles/redondantes
Aho Corasick
L'automate de Aho-Corasick associé à un ensemble de mots $X$ est décrit par :
- l'arbre associé à $X$ (comment le représenter ?)
- la fonction de suppléance $f$ (représentée dans le graphe par des arcs non étiquetés); voir ci-après
- la fonction de sortie $s$ qui associe à chaque état $u$ de $\text{Pref}(X)$ l'ensemble des mots $p$ de $X$ qui sont suffixes de $u$ (= les occurrences)
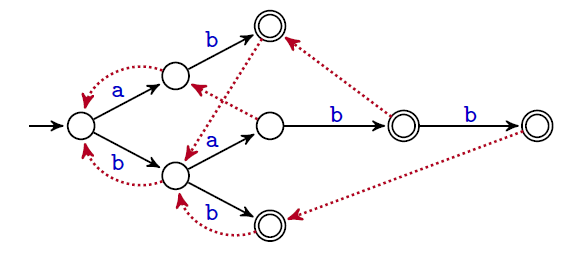
Important Cet automate est aussi important conceptuellement : il représente l'ensemble des corrélation entre les mots
Aho Corasick
Fonction de suppléance
La fonction de suppléance $f:\text{Pref}(X)\backslash\{\varepsilon\}\mapsto \text{Pref}(X)$ est définie par :$f(u)$ est le plus long suffixe propre de $u$ dans $\text{Pref}(X)$

Remarque : La fonction de suppléance pour un mot seul correspond aux bords maximaux
Aho Corasick


Comment retrouver les transitions $\delta(p,x)$ de l'automate arbre avec la fonction de suppléance $f$ ?
La définition \[ \delta(p,x)= \begin{cases} px&\text{si $px\in \text{Pref}(X)$}\\ \text{le plus long suffixe propre de $px \in \text{Pref}(X)$}&\text{sinon} \end{cases} \] se traduit en \[ \delta(p,x)= \begin{cases} px&\text{si $px\in \text{Pref}(X)$}\\ \delta(f(p),x)&\text{si $p\neq\varepsilon$ et $px\notin \text{Pref}(X)$}\\ \varepsilon&\text{si $p=\varepsilon$ et $x\notin \text{Pref}(X)$} \end{cases} \]
Aho Corasick
Recherche

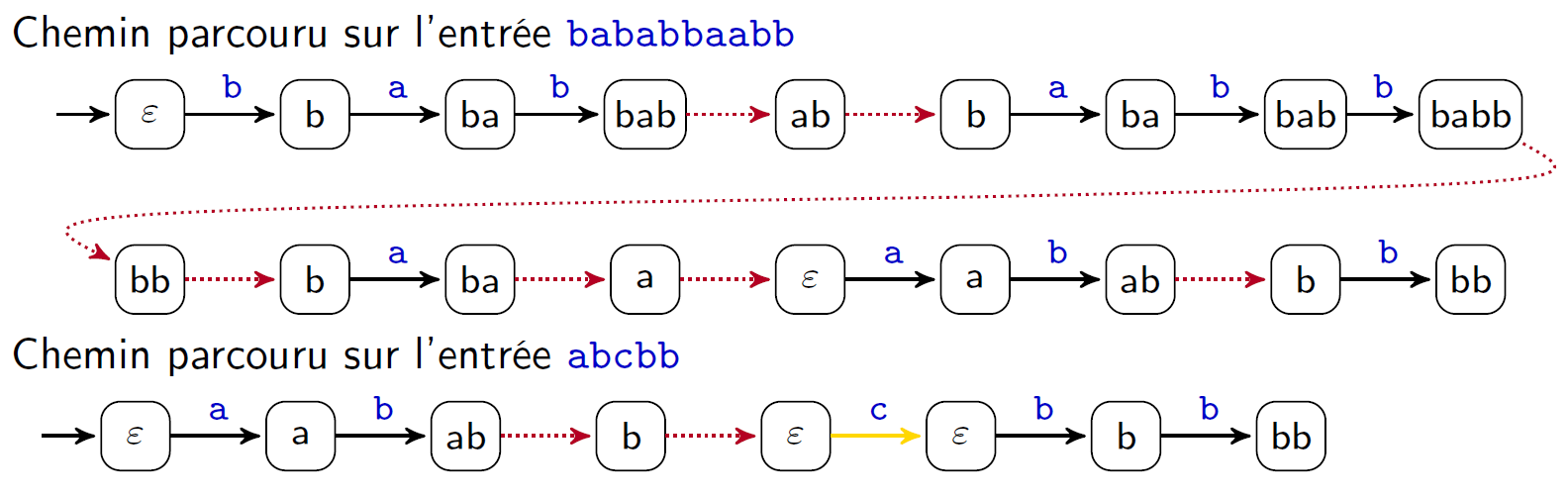
Pour un texte $t$ de longueur $n$, le chemin parcouru est de longueur au plus $2n$
- traverse $n$ arcs de l'arbre
- traverse au plus $n$ liens de suppléance (on ne peut pas remonter dans l'arbre plus de fois qu'on ait descendu)
Aho-Corasick
Considérations algorithmiques (et implantation)
À partir de l'ensemble des mots $X$, on doit construire :
- l'arbre lexicographique (tableaux de pointeurs, arbre binaire grâce à la bijection classique, table d'association, wavelet trees)
- la fonction de suppléance (définition croisée)
- la fonction de sortie (facile)

Aho-Corasick
Fonction de suppléance

La fonction de suppléance $f$ et la fonction de transition $\delta$ ont des définitions croisées : \begin{align*} f(ux)&=\left\{\begin{array}{ll} \delta(f(u),x)&\text{si }u\neq\varepsilon\\ \varepsilon&\text{si $u=\varepsilon$ (par convention)} \end{array}\right.\\ \delta(p,x)&=\left\{\begin{array}{ll} px&\text{si }px\in \text{Pref}(X)\\ \delta(f(p),x)&\text{si }p\neq\varepsilon\text{ et }px\notin \text{Pref}(X)\\ \varepsilon&\text{si }p=\varepsilon\text{ et }x\notin \text{Pref}(X) \end{array}\right. \end{align*} Grâce à un parcours en largeur de l'arbre : tout ce qu'il faut en temps utile pour construire $f$ → Pré-calcul en $O(n)$
Remarque : la fonction de suppléance peut être «optimisée» (idem bord vs bord strict)
Quelques références
- Algorithmique du texte (Crochemore, Hancart, Lecroq)
- Jewels in stringology (Crochemore, Rytter)
- http://www-igm.univ-mlv.fr/~lecroq/string/ (Lecroq, Charras)
- Des analyses en moyenne (cf M. Régnier): Boyer-Moore, Morris-Pratt, Knuth-Morris-Pratt
- Représentations compressés de l'automate de Aho-Corasick (Belazzoughi 2017...)
- (liste vraiment non exhaustive)
Indexation
Partie 2
Edgar Allan Poe, “The Gold-Bug”, Dollar Newspaper (Philadelphia, PA) June, 1843


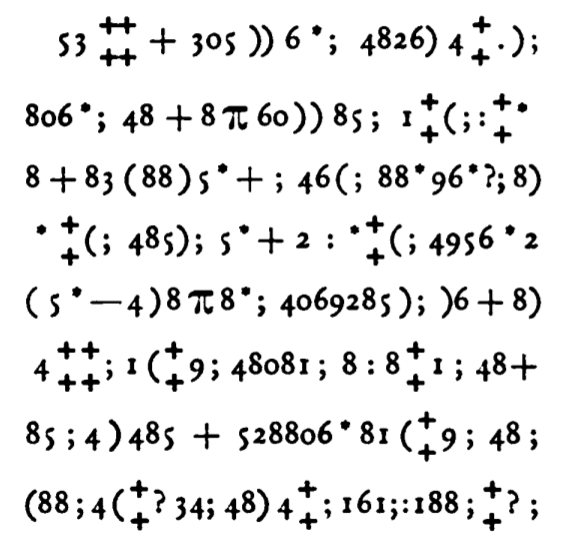
Déchiffrer grâce aux fréquences des lettres : «A good glass in the bishop's hostel in the devil's seat twenty-one degrees and thirteen minutes northeast and by north main branch seventh limb east side shoot from the left eye of the death's-head a bee line from the tree through the shot fifty feet out.»
→ L'intérêt pour les occurrences dans les textes a une longue histoire
Indexation
Trouver les occurrences d'un motif $u$ dans un texte $t$, lorsque le texte $t$ est fixe.
Applications
statistique sur le texte, trouver des répétitions ou des régularités/irrégularités, compression du texte...
Indexation
Différentes façons de représenter l'index d'un texte :
- arbre des suffixes
- table des suffixes
- transformée de Burrows-Wheeler
Objectif
Utilisée pour des textes de grande taille, la structure d'indexation doit être économe. On voudrait :- une occupation mémoire linéaire en la taille du texte
- une construction également en temps linéaire
La structure construite une fois pour toute, la recherche de motif dans le texte doit se faire en temps linéaire (ou quasi-linéaire) en la taille du motif
Trie des suffixes
Convention pratique
On ajoute à la fin du texte $t$ un caractère $\$$ distinct de tous les autres caractères du texte.
Ce marqueur $\$$ garantit :
- qu'aucun suffixe de $t$ n'est préfixe d'un autre suffixe de $t$
- une correspondance univoque entre les suffixes du texte $t$ et les feuilles du trie des suffixes de $t\$$.
Trie des suffixes
texte : $ababbb$
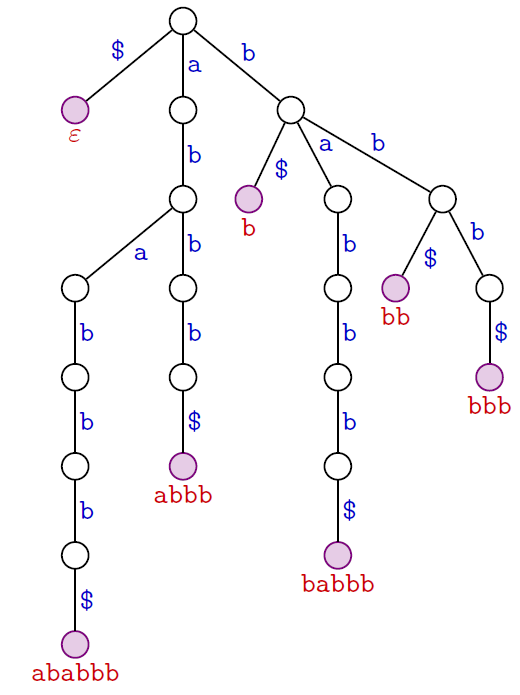
Le trie des suffixes du texte $a^4b^4$ possède $(4 + 1)2=10$ noeuds internes
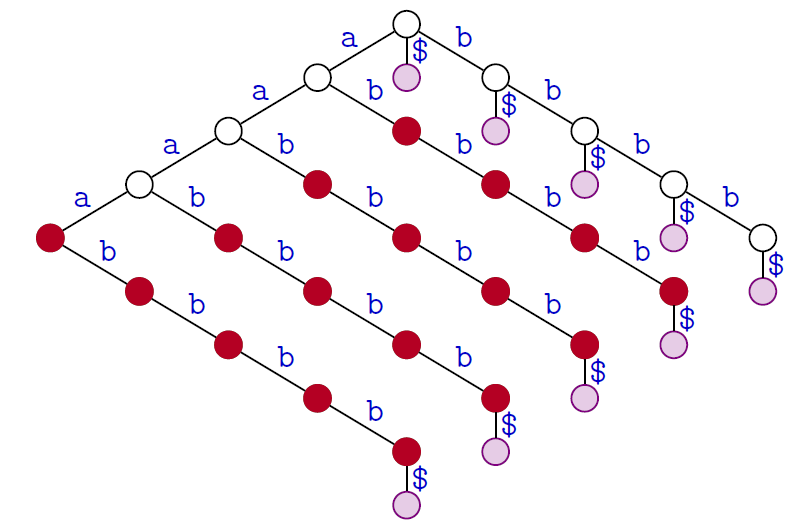
Le nombre de nœuds est quadratique en la taille du texte :
c'est trop !
→ Éliminer les nœuds de degré sortant $1$
Trie des suffixes → Arbre des suffixes
Une version compacte du trie ($\sim$ arbre PATRICIA « Practical Algorithm To Retrieve Information Coded In Alphanumeric »)
- On conserve les nœuds internes qui sont des branchements (de degré sortant au moins $2$) et les feuilles.
- Les étiquettes des arcs sont maintenant des facteurs de $t$.
L'arbre des suffixes de $t = a^4b^4$
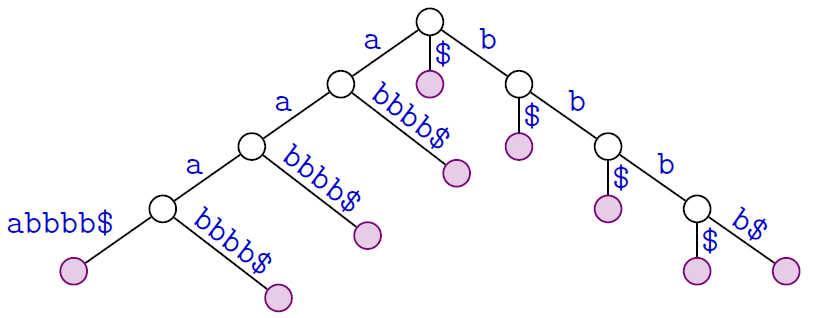
Arbre des suffixes
Complexité en espace
Le nombre de nœuds d'un arbre des suffixes est linéaire en la taille du texte
Preuve
- autant de feuilles que de suffixes
- tous les nœuds internes sont branchants
Pour un texte $t$ de longueur $n$, le nombre de nœuds de l'arbre des suffixes est d'au plus $2n$
Mais l'ensemble des étiquettes consomme un espace en $O(n^2)$ caractères. C'est trop !
Arbre des suffixes
Question
Comment coder l'ensemble des $O(n)$ étiquettes avec un espace linéaire (en $O(n))$?On stocke le texte $t$ et on code chaque étiquette (un facteur de $t$) via les deux indices debut et fin délimitant une plage du facteur dans $t$.
$t=aaaabbbb$

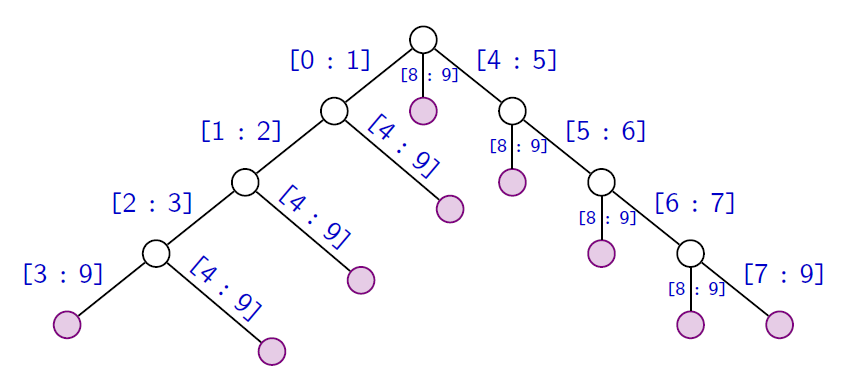
Construction de l'arbre des suffixes
Méthode naïve
Complexité en temps $O(n^2)$
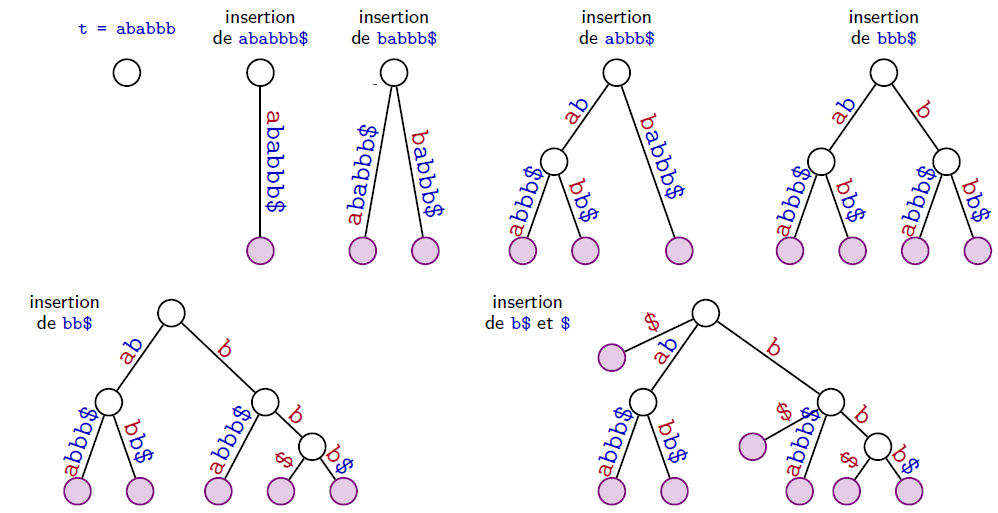
Construction de l'arbre des suffixes
Plusieurs méthodes de construction (élaborées) en $O(n)$
- Weiner (1973)
- McCreight (1976)
- Ukkonen (1995)
On doit ajouter des liens → les liens suffixes
Pour un nœud d'étiquette $au$, le lien suffixe pointe vers le nœud d'étiquette $u$.
- définis pour les nœuds branchants (avec au moins deux fils)
- accélère la navigation pour un temps de construction $O(n)$
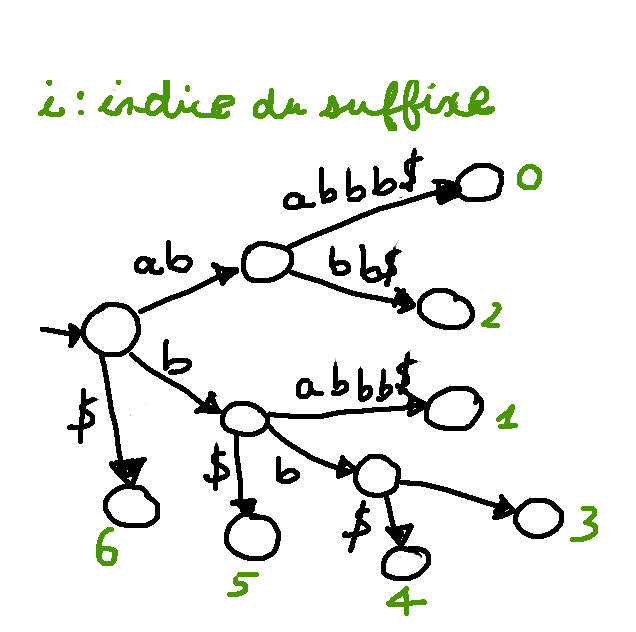
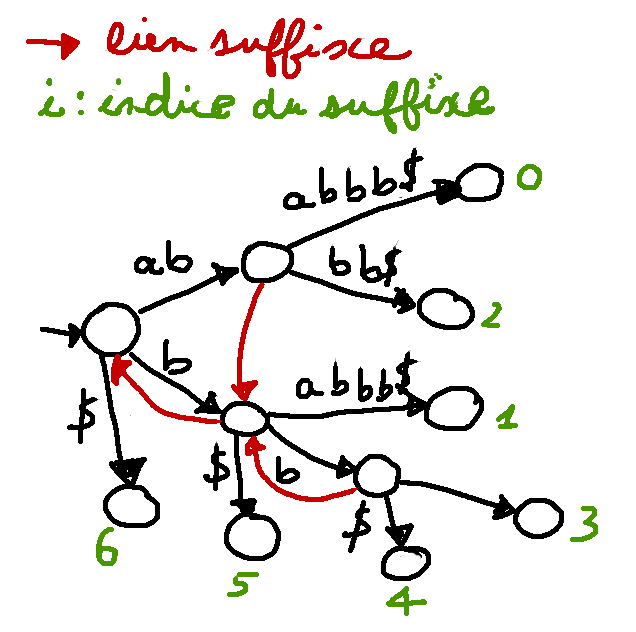
Arbre de suffixes
Recherche exacte
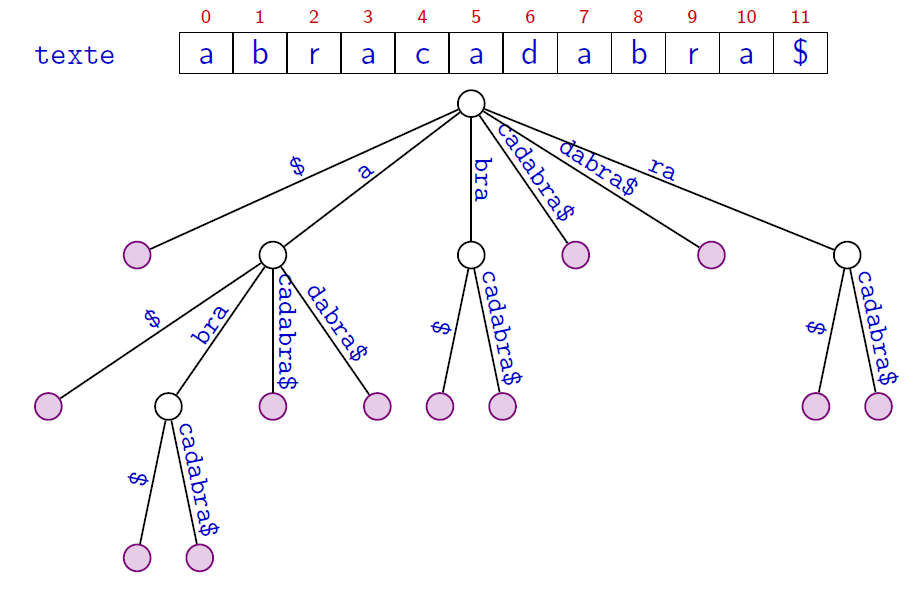
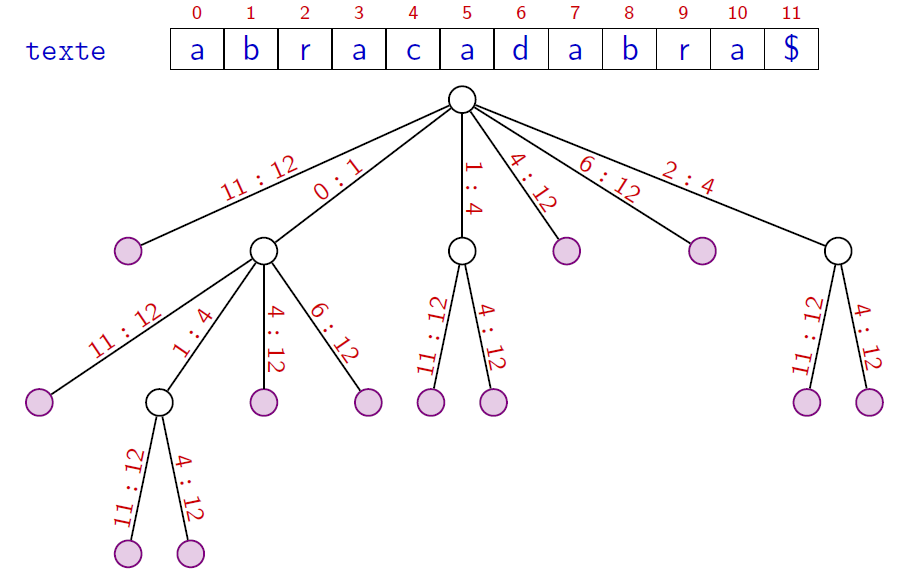
- Les motifs $bra$, $braca$, $acab$ sont ils dans le texte ?
- Comment déterminer le nombre d’occurrences ? la position ?
Arbre de suffixes (exemples d'applications)
Les plus longs facteurs qui apparaissent deux fois
L’arbre des suffixes associé au texte TCCATCATCC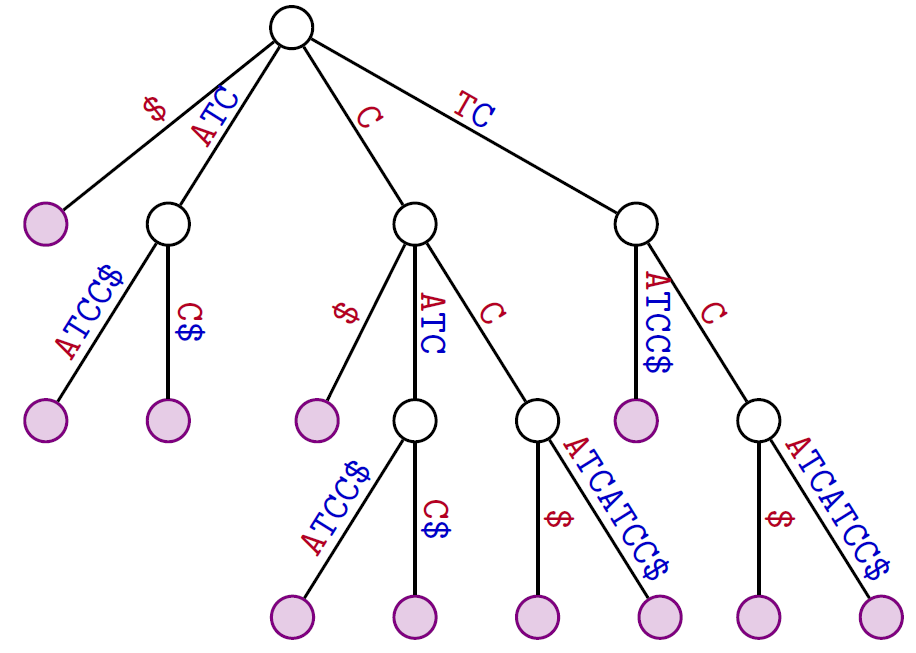
Schéma de l'algorithme :
Avec un parcours (en largeur ou en profondeur) de l'arbre des suffixes de $t$,
déterminer le(s) nœud(s) interne(s) de profondeur maximale
(ici profondeur : longueur de l'étiquette du nœud)
Le noeud d'étiquette CTAC a la profondeur maximale → CATC plus long facteur répété
Complexité
Parcours de l'arbre $O(n)$
Arbre de suffixes (exemples d'applications)
Le nombre de facteurs distincts
L’arbre des suffixes associé au texte TCCATCATCC

Avec un parcours de l'arbre des suffixes de $t$, faire la somme les longueurs des étiquettes des arcs (on omet les marqueurs $\$$)
Complexité
Parcours de l'arbre $O(n)$
Arbre de suffixes
Avantages :
algorithmes assez faciles à concevoir, l'information est facilement accessible
Inconvénients :
structure de données un peu lourde (texte à stocker, structure arborescente, gestion des pointeurs, liens suffixes)
C'est super... mais en pratique on préfère souvent la table des suffixes !
Indexation
Table de suffixes (suffix array)
Conçu par Manber & Myers (1993)
Avantages de la table
-
structure très simple, utilise moins d'espace que l'arbre des suffixes
- performance en temps comparable à celle de l'arbre des suffixes
Conçu par Manber & Myers (1993)
Avantages de la table
- structure très simple, utilise moins d'espace que l'arbre des suffixes
- performance en temps comparable à celle de l'arbre des suffixes
suffixes du texte triés en ordre lexicographique
le texte : $t=abracadabra$ ($|t|=11$)
la liste des suffixes non vides
| $i$ | $t|i..n-1]$ |
|---|---|
| 0 | abracadabra |
| 1 | bracadabra |
| 2 | racadabra |
| 3 | acadabra |
| 4 | cadabra |
| 5 | adabra |
| 6 | dabra |
| 7 | abra |
| 8 | bra |
| 9 | ra |
| 10 | a |
la liste triée
| $i$ | $t[TS[i]..n-1]$ | $TS[i]$ |
|---|---|---|
| 0 | a | 10 |
| 1 | abra | 7 |
| 2 | abracadabra | 0 |
| 3 | acadabra | 3 |
| 4 | adabra | 5 |
| 5 | bra | 8 |
| 6 | bracadabra | 1 |
| 7 | cadabra | 4 |
| 8 | dabra | 6 |
| 9 | ra | 9 |
| 10 | racadabra | 2 |
Table de suffixes
Définition
$TS[i]$ est la position du i-ème suffixe de $t=t[0..n-1]$ dans l'ordre lexicographique \[ t[TS[i]..n-1]\leq_{lex} t[TS[i+1]..n-1] \] \[
a\leq_{lex} abra\leq_{lex} abracadabra \leq_{lex} acadabra\leq_{lex}\cdots
\]
\[
a\leq_{lex} abra\leq_{lex} abracadabra \leq_{lex} acadabra\leq_{lex}\cdots
\]
L'inverse de la table des suffixes (c'est la permutation inverse)
\[
ITS[i]=j \Leftrightarrow TS[j]=i
\]
→ $ITS[i]$ le rang dans l'ordre lexicographique du suffixe $t[i..n-1]$

Construction de la table des suffixes
- Construction naïve : trier les $n$ suffixes du texte.
Coût en $O(n^2 \log(n))$
Le tri effectue $O(n \log(n))$ comparaisons et chaque comparaison a un coût en $O(n)$ - À partir de l'arbre des suffixes
Coût en temps en $O(n)$- construire l'arbre des suffixes : coût en $O(n)$
- parcours préfixé dans l'ordre lexicographique de l'arbre : coût en $O(n)$
- Construction directe
Plusieurs algorithmes assez élaborés ont un coût en temps et en espace en $O(n)$
- Kärkkäinen et Sanders (2003)
- Ko et Aluru (2003)
- Nong, Zhang, Chan (2009)
Ces méthodes directes sont un grand progrès !
(Auparavant, en pratique, méthodes de tri en $O(n \log n)$)
Regardons plus en détails l'algorithme de Kärkkäinen et Sanders
L'algorithme dissymétrique de Kärkkäinen et Sanders
Tri des suffixes basée sur une stratégie de type ``diviser pour régner''
On partage les suffixes du texte en deuxet l'on procède en trois étapes :
- On construit la table $TS^{12}$ résultant du tri de $\text{Suff}^{12}$ en se ramenant à la construction de la table des suffixes d'un mot de longueur réduite au $2/3$ de la longueur initiale
- On construit la table ${TS^{0}}$ résultant du tri de $\text{Suff}^{0}$ en utilisant la table ${TS^{12}}$ construite à l'étape précédente
- On fusionne les deux tables ${TS^{0}}$ et ${TS^{12}}$ en utilisant à nouveau la table ${TS^{12}}$
L'algorithme dissymétrique de Kärkkäinen et Sanders
Un ingrédient important : tri par comptage (base du tri radix)
- Entrée : une liste de taille $n$ d'éléments d'un ensemble $\Sigma$ ordonné
- Sortie : la liste triée
Principe :
- Première passe : on compte effectifs des symboles de l'alphabet
- Deuxième passe : on affecte les éléments à leur bonne place
Si l'ensemble $\Sigma$ est supposé de taille constante, le tri s'effectue en temps et espace « linéaire » $O(n)$.
def countsort(a, b, n, k) : # a est un tableau de n entiers de 1..k, b sera le tableau trié
c = array("i", [0]*(k+1)) # tableau pour compter les effectifs
for i in range(n) : # on compte les effectifs c[k] = nombre de symboles k dans a
c[a[i]]+=1
somme = 0 # on calcule les effectifs cumulés c[k] = nombre de symboles < k dans a
for i in range(k+1):
freq, c[i] = c[i], somme
somme += freq
for i in range(n) : # on remet les choses à leur place
b[c[a[i]]]] = a[i]
c[a[i]] += 1
L'algorithme dissymétrique de Kärkkäinen et Sanders
Étape 1. Construire la table ${TS^{12}}$
$w=agctctctttt$ → $w=agctctctttt\textcolor{green}{\$\$}$

L'algorithme dissymétrique de Kärkkäinen et Sanders
Étape 1. Construire la table ${TS^{12}}$
On ne garde que les suffixes $w[i..n-1]$ avec $i \mod 3 \not=0$
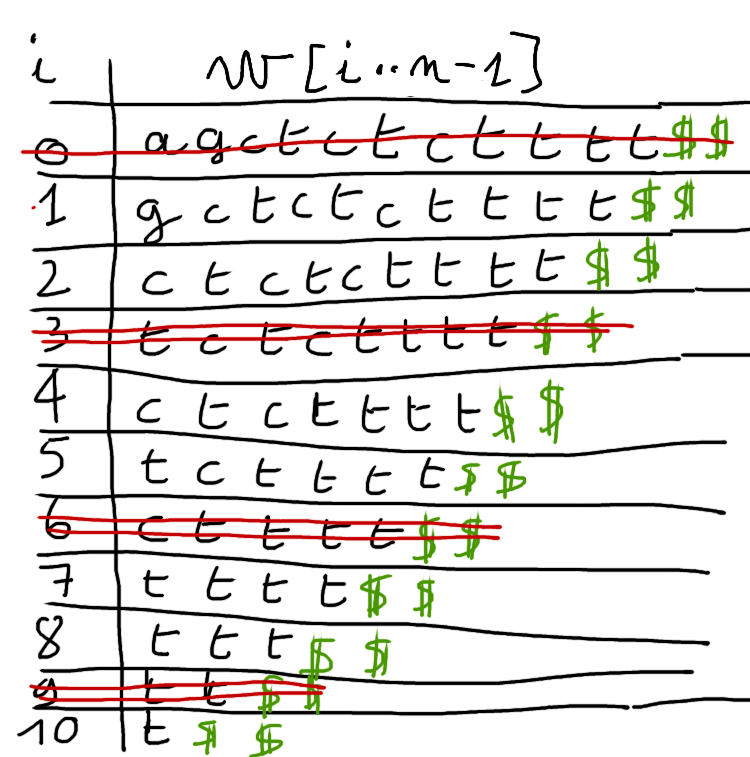

L'algorithme dissymétrique de Kärkkäinen et Sanders
Étape 1. Construire la table ${TS^{12}}$
on trie dans l'ordre lexicographique les facteurs de longueur $3$ débutant aux positions $i \mod 3 \neq 0$ → tri radix (3 passes) qui s'effectue en temps linéaire.
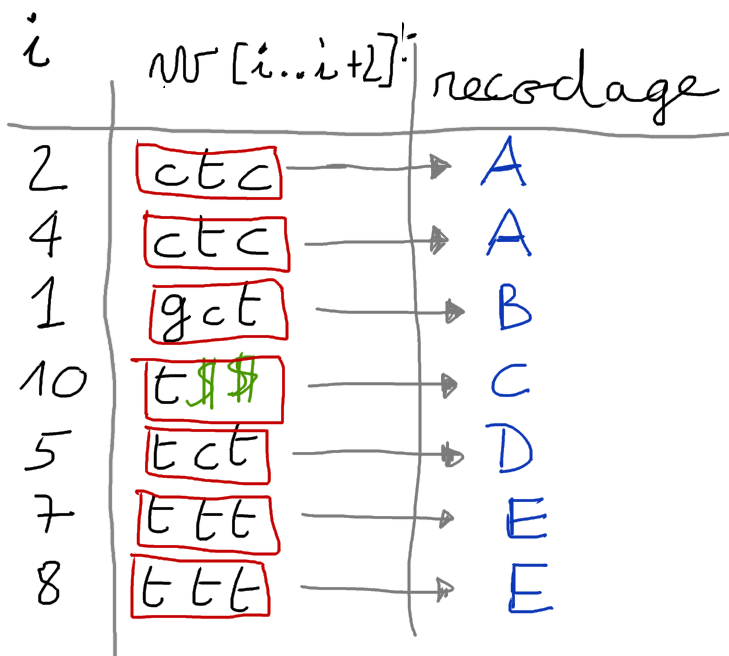
Si les facteurs sont tous distincts, c'est terminé : on obtient directement la table ${TS^{12}}$
Dans le cas général, on recode chaque facteur de longueur 3 (par rapport à son rang dans l'ordre lexicographique)
L'algorithme dissymétrique de Kärkkäinen et Sanders
Étape 1. Construire la table ${TS^{12}}$
À partir de ce renommage
\[
ctc\rightarrow A, gct\rightarrow B, t\$\$\rightarrow C, tct\rightarrow D, $ttt\rightarrow E,
\]
on construit un nouveau texte $w'$, concaténation des rangs des facteurs en position $i \mod 3 =1$ suivis des rangs des facteurs en position $i \mod 3 =2$.
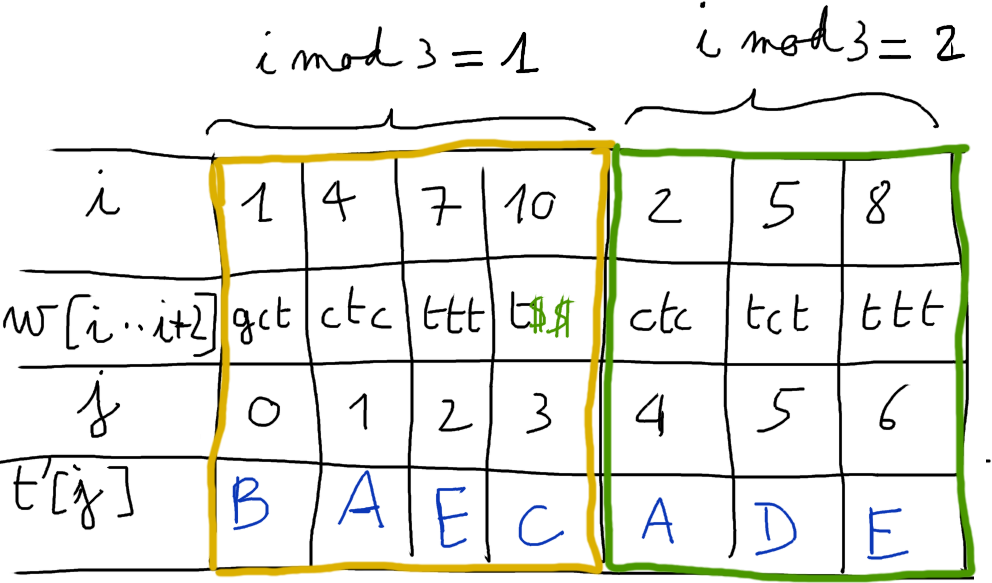
Ce texte $w' = BAECADE$ a une taille réduite au $2/3$ de la taille du texte initial.
L'algorithme dissymétrique de Kärkkäinen et Sanders
Étape 1. Construire la table ${TS^{12}}$
On construit la table des suffixes $TS'$ de $w'$ en appliquant de manière récursive l'algorithme sur $w'$.
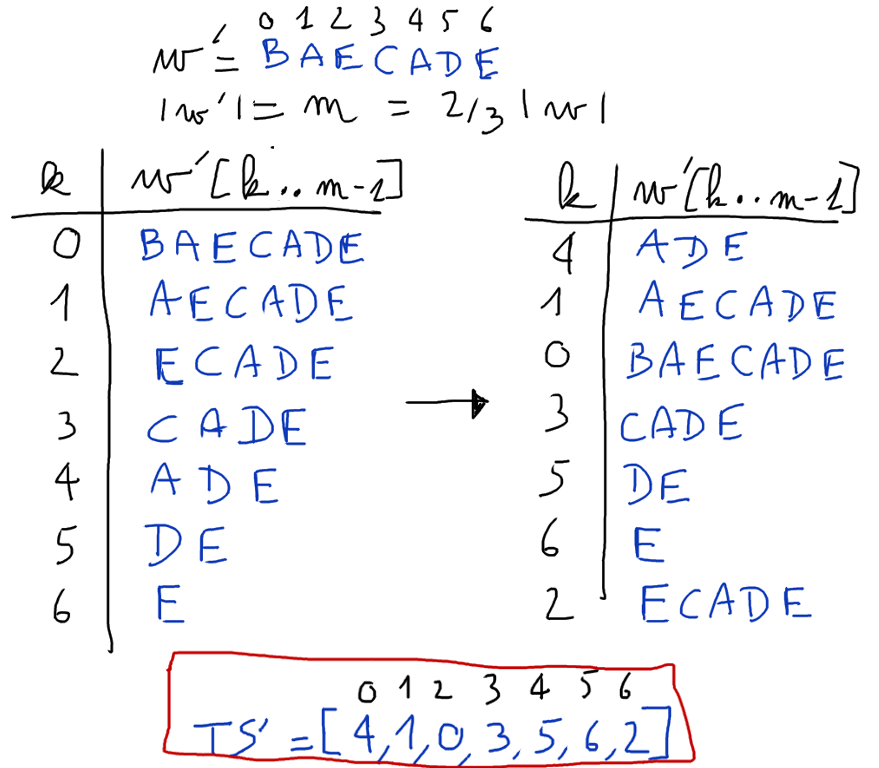
L'algorithme dissymétrique de Kärkkäinen et Sanders
Étape 1. Construire la table ${TS^{12}}$
La table des suffixes de $w'$ correspond à la table $TS^{12}$ que l'on veut construire.
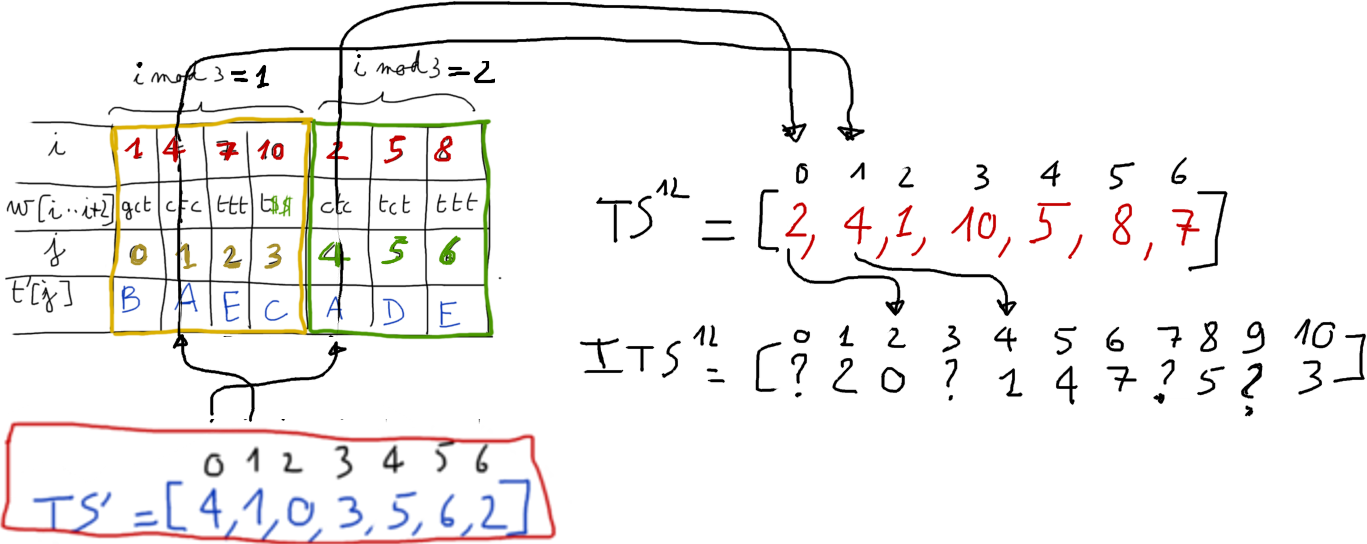
L'algorithme dissymétrique de Kärkkäinen et Sanders
Étape 2. Construire la table ${TS^{0}}$
Il s'agit de trier les suffixes qui débutent aux positions multiples de $3$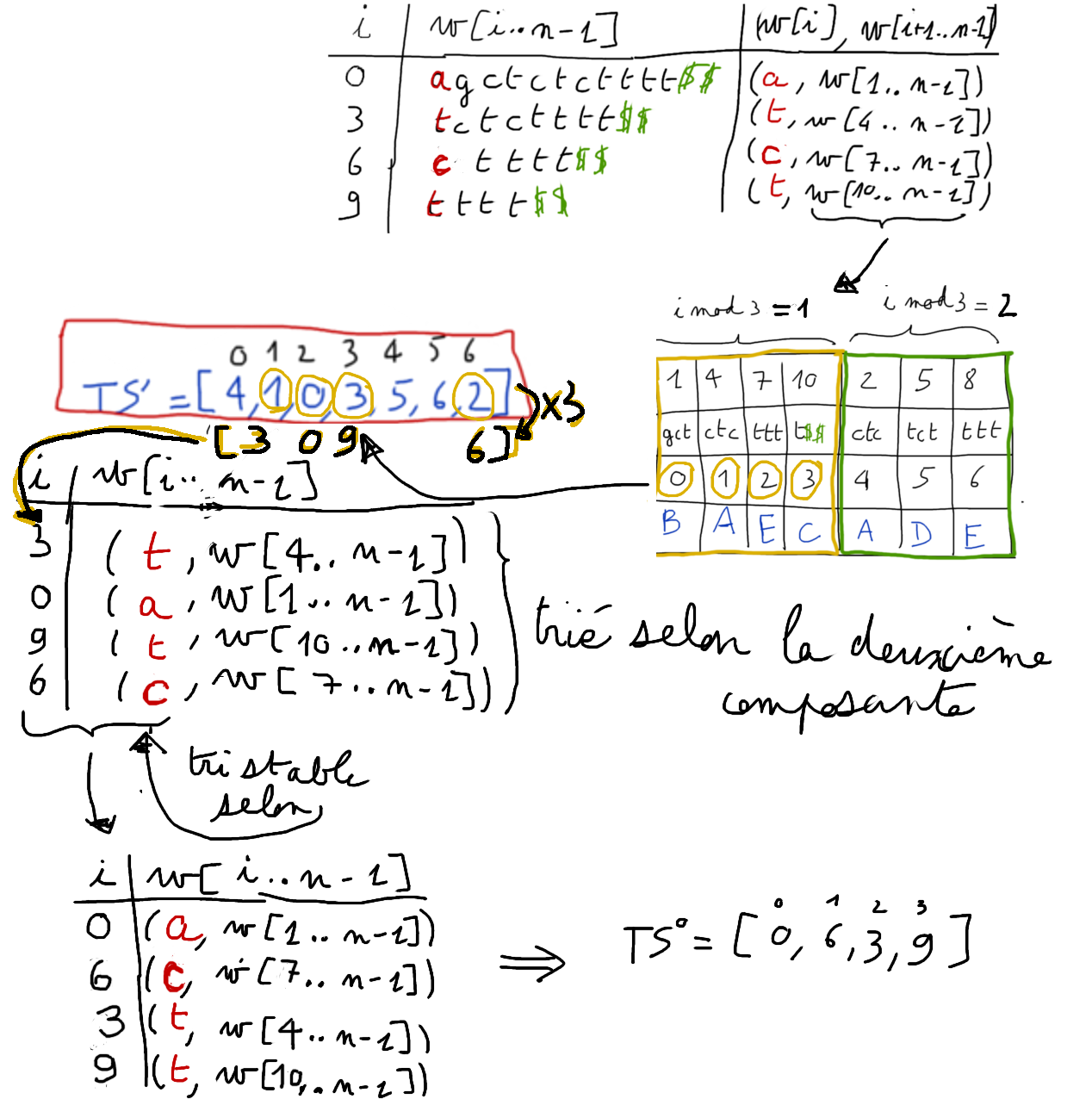
L'algorithme dissymétrique de Kärkkäinen et Sanders
Etape 3. Fusion de $TS^{0}$ et $TS^{12}$
$w=agctctctttt$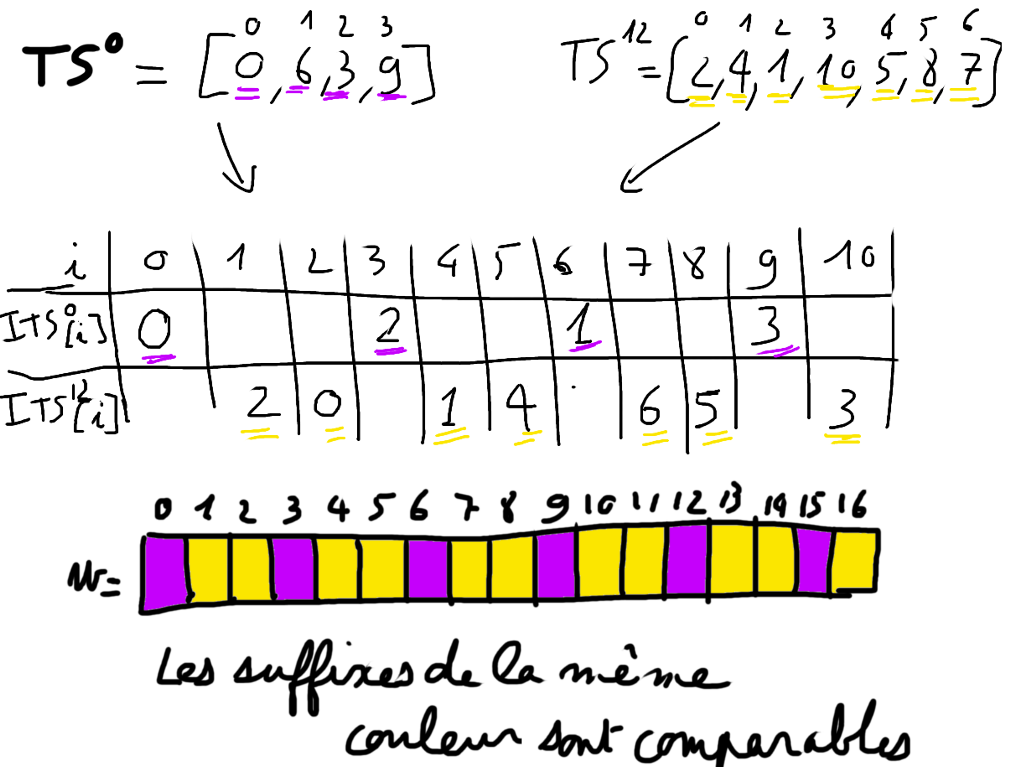
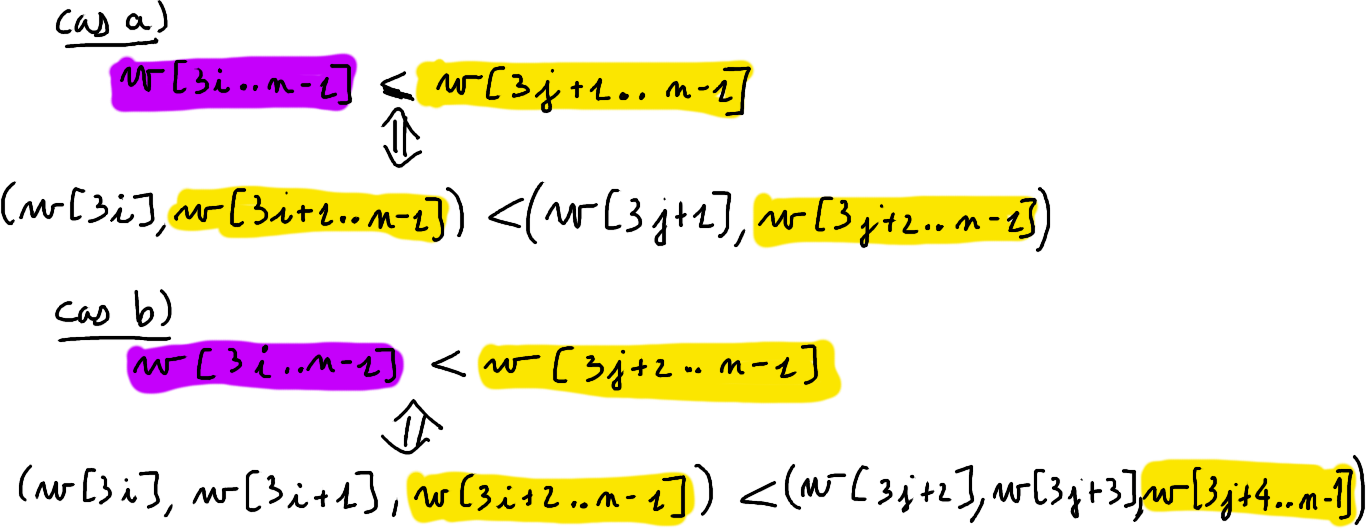
L'algorithme dissymétrique de Kärkkäinen et Sanders
Etape 3. Fusion de $TS^{0}$ et $TS^{12}$

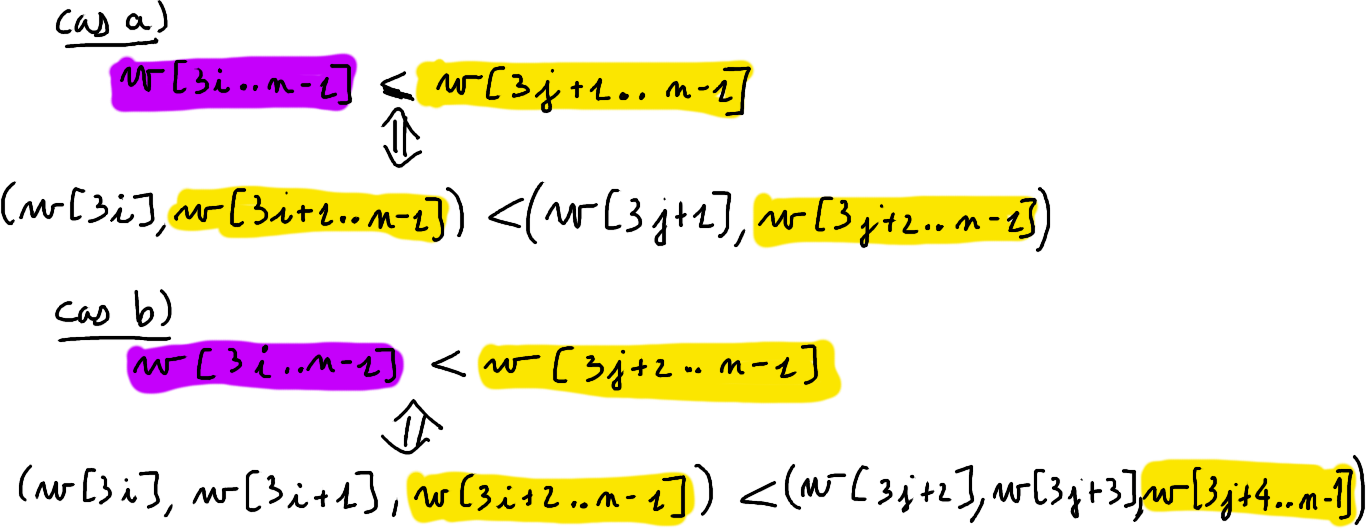
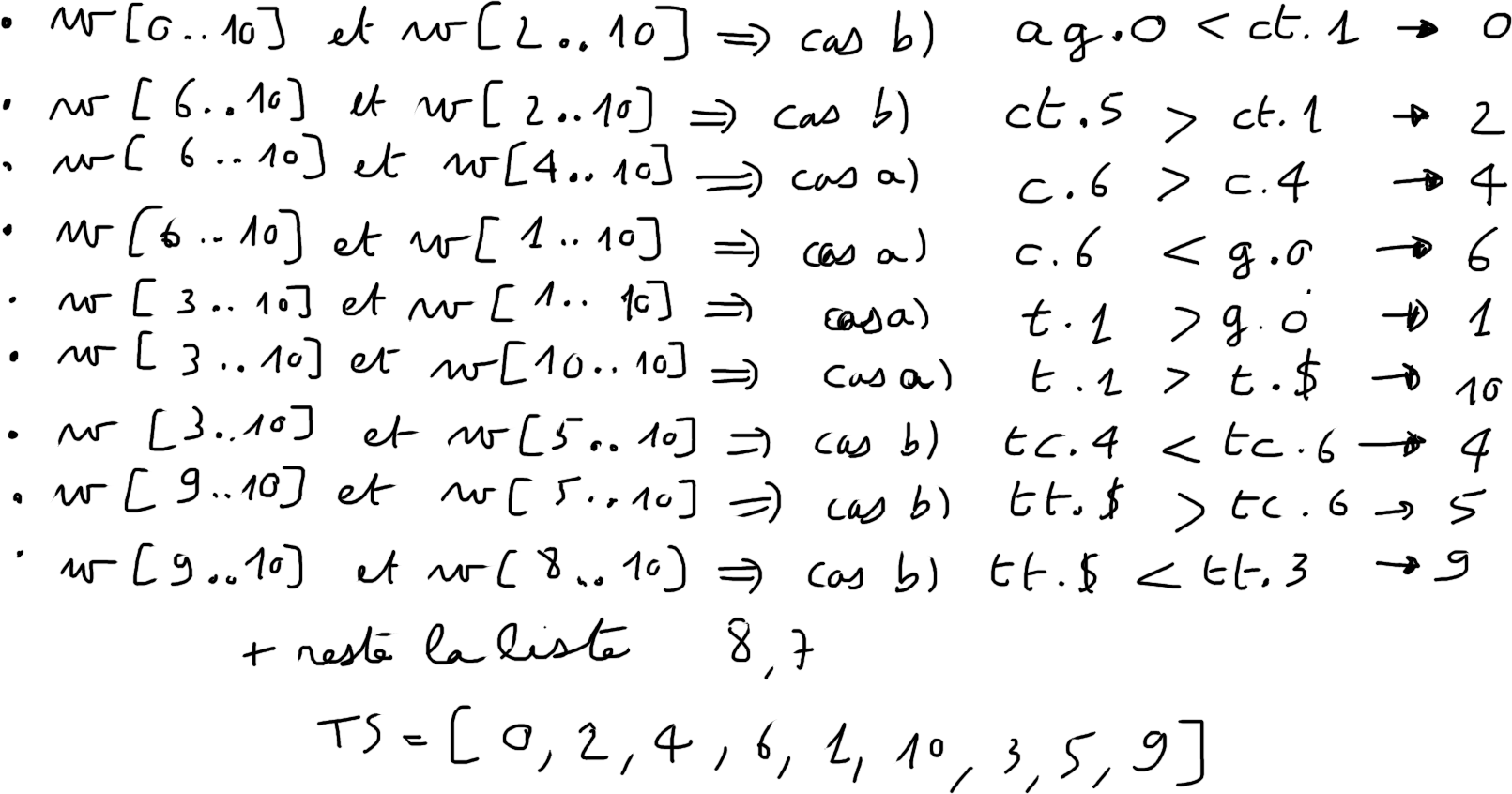
L'algorithme dissymétrique de Kärkkäinen et Sanders
Complexité
Évaluons $T(n)$ la complexité en temps de l'algorithme pour un texte de longueur $n$.Les opérations réalisées et leur coût :
- Tri des suffixes pour les positions non multiples de $3$
- Extraire les facteurs $texte[i..i+2]$ avec $i \mod 3 \neq 0$ en ${O(n)}$
- Tri des facteurs (un tri radix à $3$ passes) en ${O(n)}$
- Renommage des facteurs en {O(n)}
- Construction de $w'$ en {O(n)}
- Appel récursif sur $w'$ de longueur $2n/3$ en {T(2n/3)}
- Tri des suffixes pour les positions multiples de $3$ + une passe d'un tri radix en {O(n)}
- Fusion des deux tables en $O(n)$
La complexité est ainsi déterminée par l'équation de récurrence (de type diviser pour régner) \[ T(n) = O(n) + T(2n/3) \]
Conclusion
l'algorithme a une complexité en $O(n)$
Table des suffixes versus Arbre des suffixes
Dans les applications mettant en jeu des textes de grande taille, la table de suffixes supplante l'arbre des suffixes :
- elle est plus économe en mémoire
- elle offre une meilleure localité spatiale qui diminue les erreurs de cache et le coût dû aux accès à la mémoire
Mais la table des suffixes seule ne permet pas de retrouver toute la structure de l'arbre des suffixes. La table des suffixes est ainsi souvent combinée avec des structures additionnelles (la table $HTR$, l'arbre d'intervalles de $HTR$...).
La table et ses structures auxiliaires restent économes en mémoire et permettent de définir l'équivalent d'un arbre des suffixes.
Une structure auxiliaire : la table $HTR$
Les préfixes communs à deux suffixes consécutifs
La table $HTR$ stocke les longueurs des préfixes communs aux éléments consécutifs dans la table des suffixes
On dénote par $\text{lcp}(s,t)$ le plus long préfixe commun aux mots $s$ et $t$ \[ \text{lcp}(\text{vélocypède},\text{vélocité}) = \text{véloc} \]
$HTR[i]$ est la longueur du plus long préfixe commun aux deux suffixes consécutifs (pour l'ordre lexicographique) indexés dans la table $TS$ par $i-1$ et $i$.
\[ HTR[i] = |\text{lcp}(t[TS[i-1]..],t[TS[i]..])| \]La construction s'effectue en temps linéaire.
Une structure auxiliaire : la table $HTR$
Exemple
La table $HTR$ du texte $abracadabra$
Une structure auxiliaire : la table $HTR$
Les profondeurs des nœuds internes dans l'arbre des suffixes
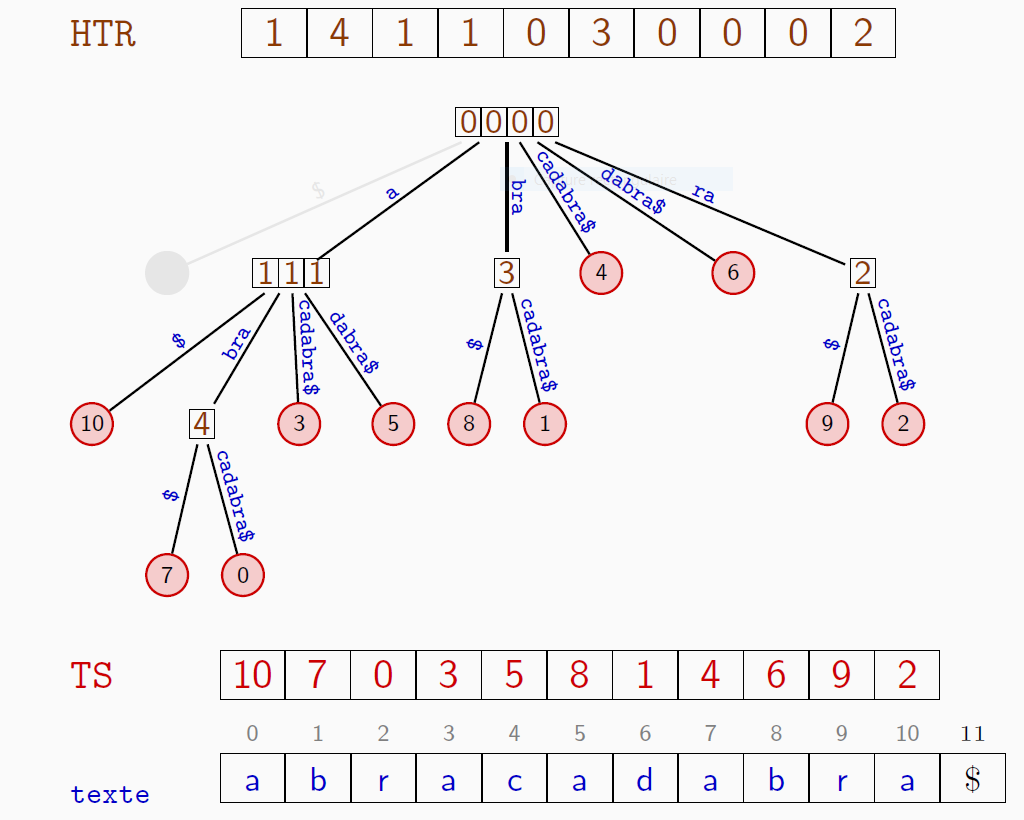
Une structure auxiliaire : la table $HTR$
Propriété La longueur du prefixe commun des suffixes de la plage $i < j$ est \[ \text{lcp}(texte[TS[i]..n-1],texte[TS[j]..n-1]) = \min\limits_{i\, <\, k \,\leq \,j}(HTR[k]) \]
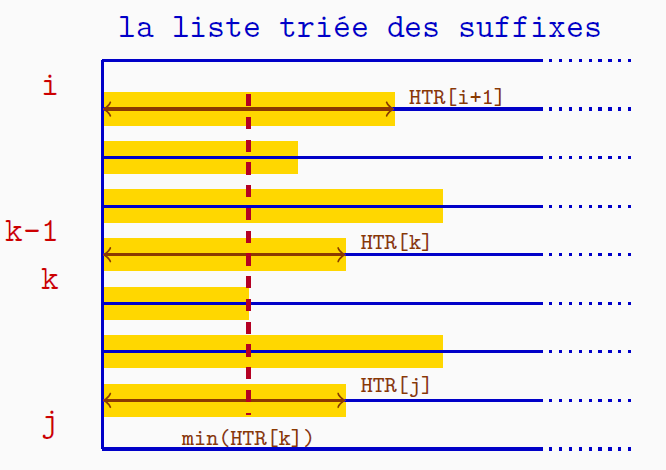
Table des suffixes : applications
Les utilisations de la table des suffixes sont multiples (et les mêmes que pour l'arbre des suffixes) :
- Recherche de motifs
- Détection des répétitions
- Recherche du plus long facteur commun à plusieurs chaînes
- Statistiques sur le texte
- Compression de texte
Examinons quelques cas concrets
Table des suffixes : applications
Détecter les répétitions d'un texte
On veut détecter le ou les plus longs facteurs répétés dans un texte.
Un facteur qui est répété, est préfixe commun de suffixes distincts. Et ces suffixes sont consécutifs dans la table des suffixes.
Les facteurs répétés les plus longs sont ainsi caractérisés par
la valeur maximale de la table $HTR$.

Il y en a $2$ (autant que le nombre de plages de valeur $4$ dans $HTR$) qui sont :
- $CGAC$ figurant aux positions $16$ et $21$
- $GACG$ figurant aux positions $2$ et $22$
Table des suffixes : applications
Détecter les répétitions d'un texte
Généralisation :
détecter le ou les plus longs facteurs qui apparaissent au moins $k$ fois dans un texte.
Pour $k = 3$ occurrences, on calcule le minimum des plages de longueur $k-1=2$ de la table $HTR$.
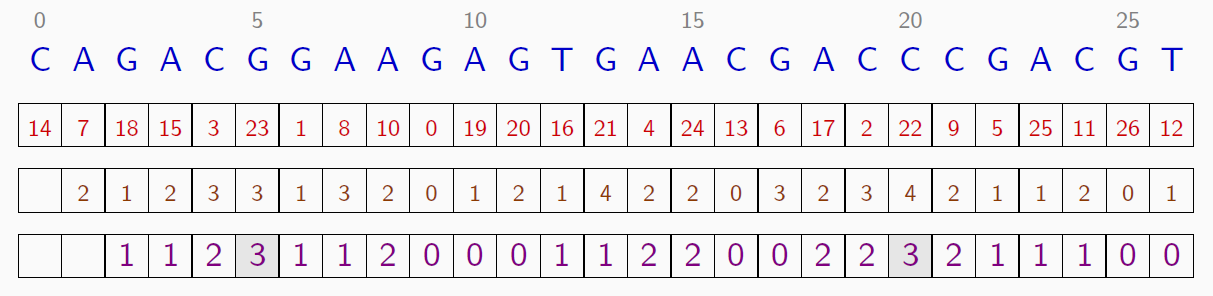
2 facteurs de longueur 3 au moins trois fois:
- $ACG$ figurant aux positions $15$, $3$ et $23$
- $GAC$ figurant aux positions $17$, $2$ et $22$
Table des suffixes : applications
Le plus long facteur commun à plusieurs chaînes
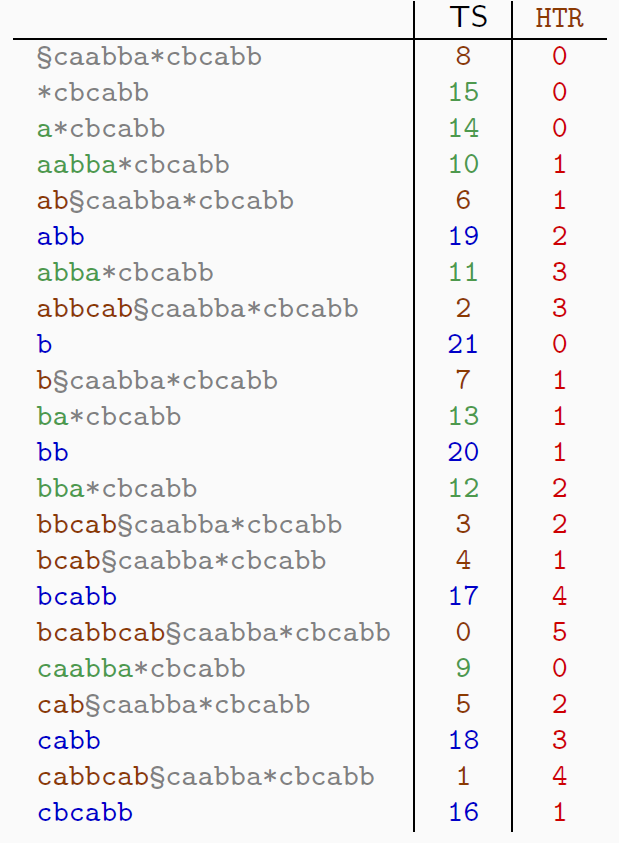
Table des suffixes : applications
Le nombre de facteurs distincts d'un texte
Un texte de longueur $n$ comprend $n(n+1)/2$ facteurs non vides
$ababbb$ possède $21=\frac{6\times 7}{2}$ facteurs :$a, b, a, b, b, b, ab, ba, ab, bb, bb, aba, bab, abb, bbb, abab, babb, abbb, ababb, babbb, ababbb$
avec $a, ab, bb$ répétés une fois et $b$ répétés trois fois.
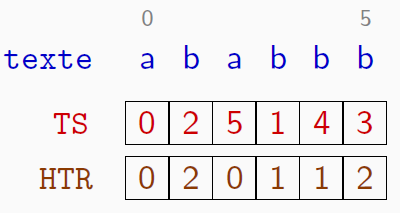
- $HTR[1]=2$ : le préfixe $ab$ est répété $\Rightarrow$ les facteurs $ab$ et $a$ sont répétés;
- $HTR[3]=1$ : $b$ est répété
- $HTR[4]=1$ : $b$ est répété;
- $HTR[5]=2$ : le préfixe $bb$ est répété $\Rightarrow$ les facteurs $bb$ et $b$ sont répétés.
Le nombre de facteurs distincts est $21 - 2 - 1 - 1 - 2 = 15$
De façon générale, le nombre de répétitions est $\sum\limits_i HTR[i]$ et le nombre de facteurs distincts est $n(n+1)/2 - \sum\limits_i HTR[i]$
Table des suffixes : applications
Détection des répétitions supermaximales
Une répétition supermaximale d'un texte est un facteur répété qui n'est facteur propre d'aucune autre répétition
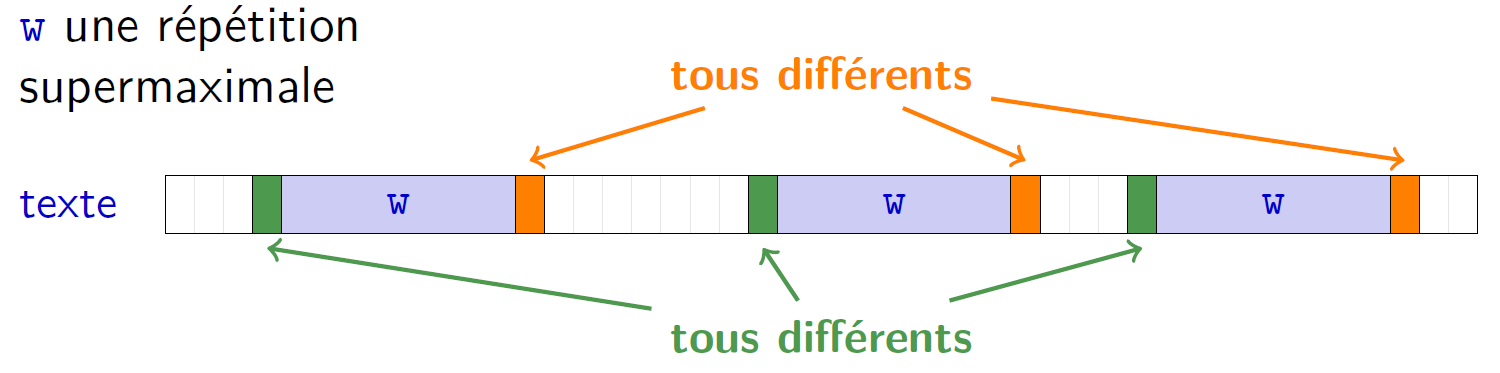
Utiliser une table de suffixes !
La stratégie :
- Dans un premier temps, déterminer les facteurs répétés qui ne sont préfixes propres d’aucune autre répétition
- Puis, filtrer ceux qui également ne sont suffixes propres d’aucune autre répétition
Table des suffixes : applications
Détection des répétitions supermaximales
sur un exemple : GATAAGATTGATG
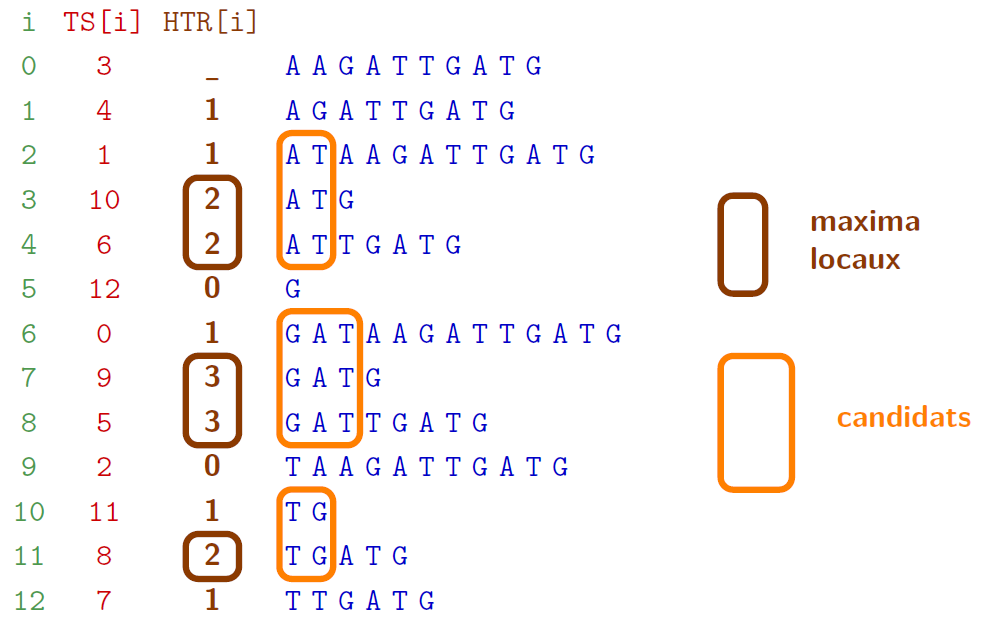
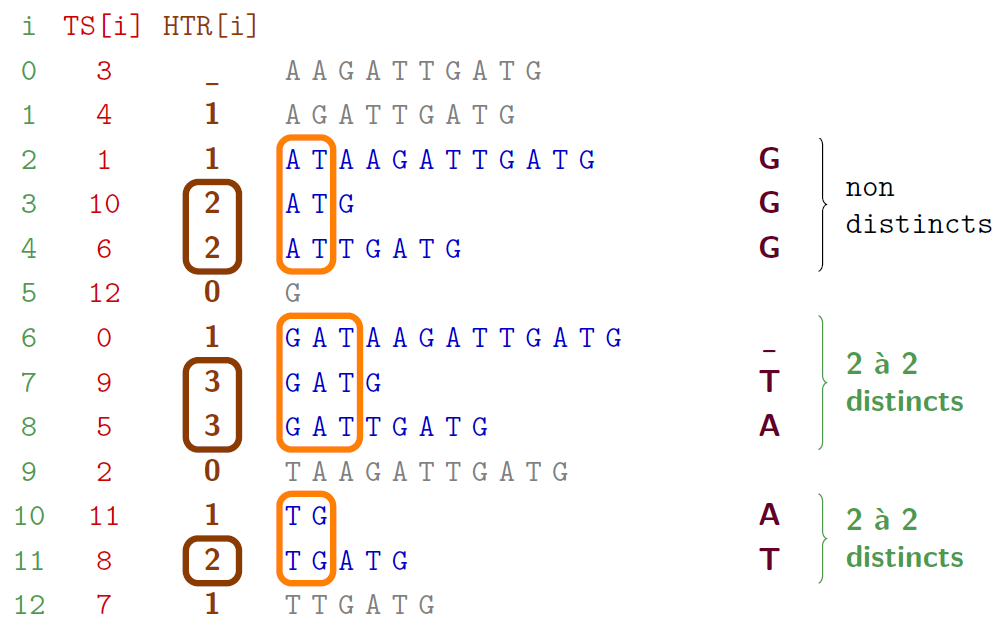
Table des suffixes : applications
Recherche de mot dans un texte
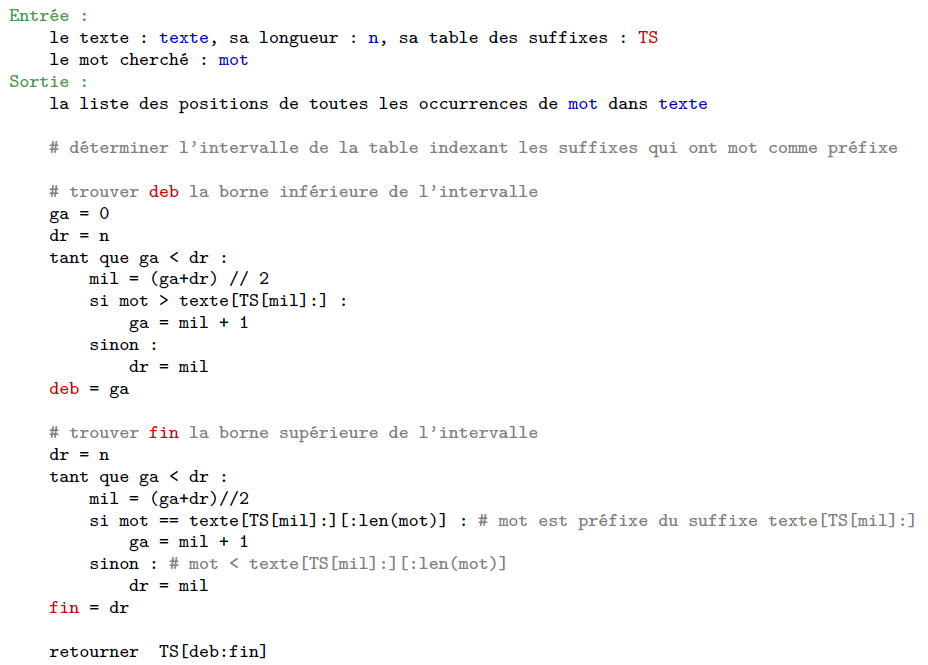
- recherche dichotomique de $u$ dans un texte $t$ : $O(|u| \times \log(|t|))$
- Utilisation judicieuse de $HTR$ et structure pour stocker les longueurs de préfixes de commun : $O(|u| \times \log(|t|))$
Auto-indexation
Transformée de Burrows-Wheeler & et FM index
Auto-indexation
Introduction
Un facteur critique : l'espace

- Les implantations pour les tables de suffixes occupent au mieux un espace de $n\log(n)$ bits pour un texte de taille $n$.
- On a en plus besoin du texte.
Et les données peuvent être grandes !
- Le génome humain : $3400$ Mega paires de nucléotides
→ $3400\times 10^6\times\log(3400\times 10^6)$ bits : $13,4$ Go - La fleur Paris japonica $150$ Giga paires de nucléotides
→ $150\times 10^9\times\log(150\times 10^9)$ bits : $3$ To
Idée : Sacrifier un peu d'efficacité au profit d'un gain d'espace, en utilisant une structure qui contient à la fois le texte et l'index.
→ FM index (Ferragina & Manzini) : Structure basée sur la transformée de Burrows-Wheeler (1994)
La transformée de Burrows-Wheeler
Description simple
Étant donné un texte $t$
- Ajouter à la fin de $t$ un marqueur $\$$ considéré comme inférieur à toute autre lettre.
- Engendrer l'ensemble des $|t|+1$ rotations (i.e., les permutations circulaires) de $t\$$ .
- Trier l'ensemble de ces rotations selon l'ordre lexicographique.
- Retourner la séquence formée du dernier caractère de chaque mot de l'ensemble trié.
La transformée de Burrows-Wheeler

La transformée de Burrows-Wheeler
Notations

- $F$ (comme First) la première colonne de la matrice des rotations triées
- $L$ (comme Last) la dernière colonne de la matrice des rotations triées, i.e., le résultat de la transformée
Remarque : trier les rotations ou trier les suffixes, c'est pareil !
La transformée de Burrows-Wheeler
Une caractéristique exploitée pour la compression de données
Les occurrences d'un même caractère dont les contextes droits sont « proches » sont regroupées
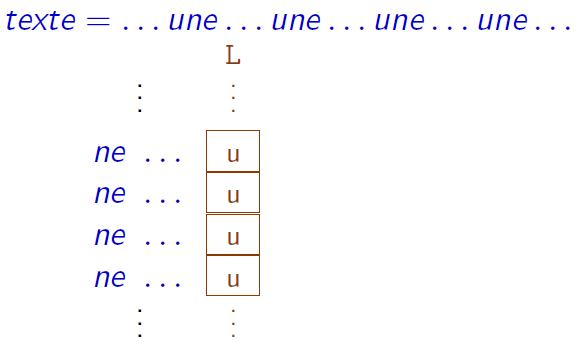
Cette transformée permet d'expliciter les redondances du texte et favorise ainsi une bonne compression.
La transformée de Burrows-Wheeler est l'étape préliminaire utilisée dans l'algorithme de compression bzip2
La transformée de Burrows-Wheeler
La transformée inverse
Après application de la transformée de Burrows-Wheeler, la séquence obtenue est o$lag. Quel est le texte initial ?
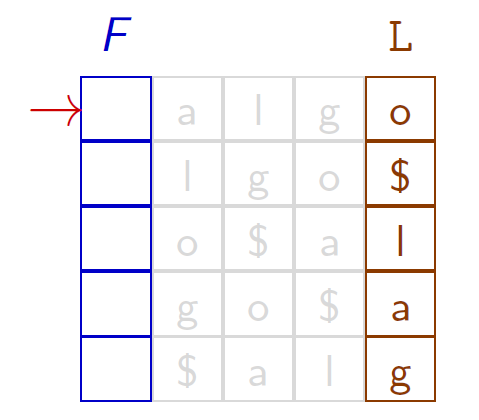
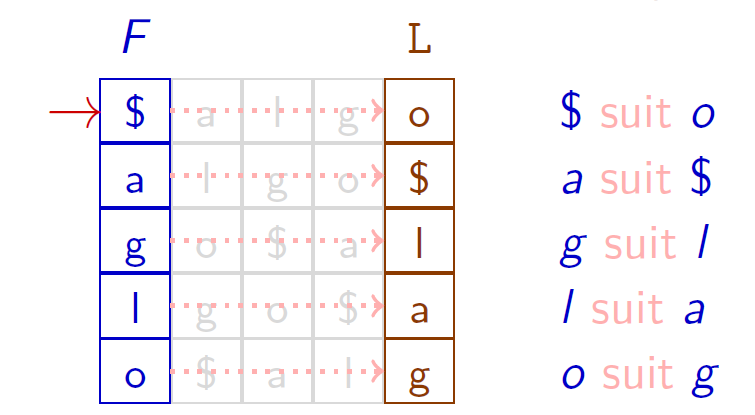
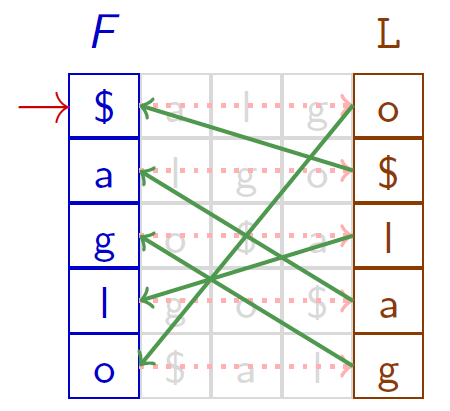
- On retrouve la première colonne $F$ = la dernière colonne $L$ triée
- On reconstruit le texte à partir des deux colonnes $F$ et $L$ :
\[
\$ \leftarrow o \leftarrow g \leftarrow l\leftarrow a \leftarrow \$
\]
Le cas est simple, tous les caractères du texte $algo$ étant distincts
La transformée de Burrows-Wheeler
La transformée inverse
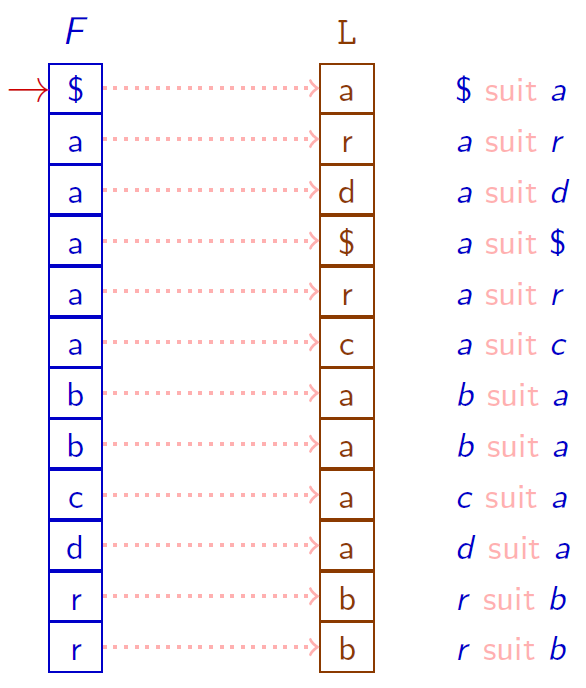
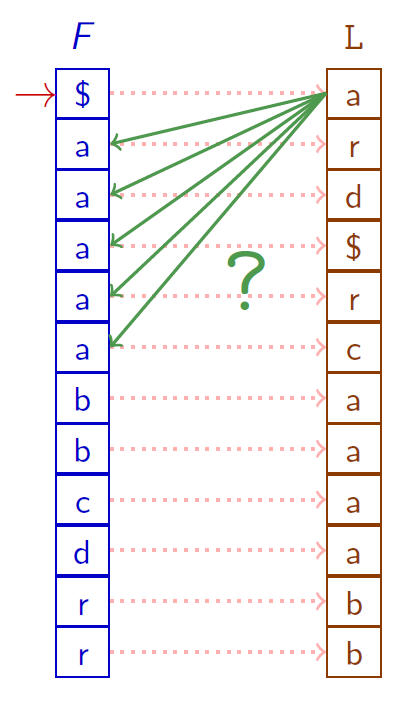
Les occurrences d'un même caractère ont le même ordre dans $F$ et dans $L$
La transformée de Burrows-Wheeler
La transformée inverse

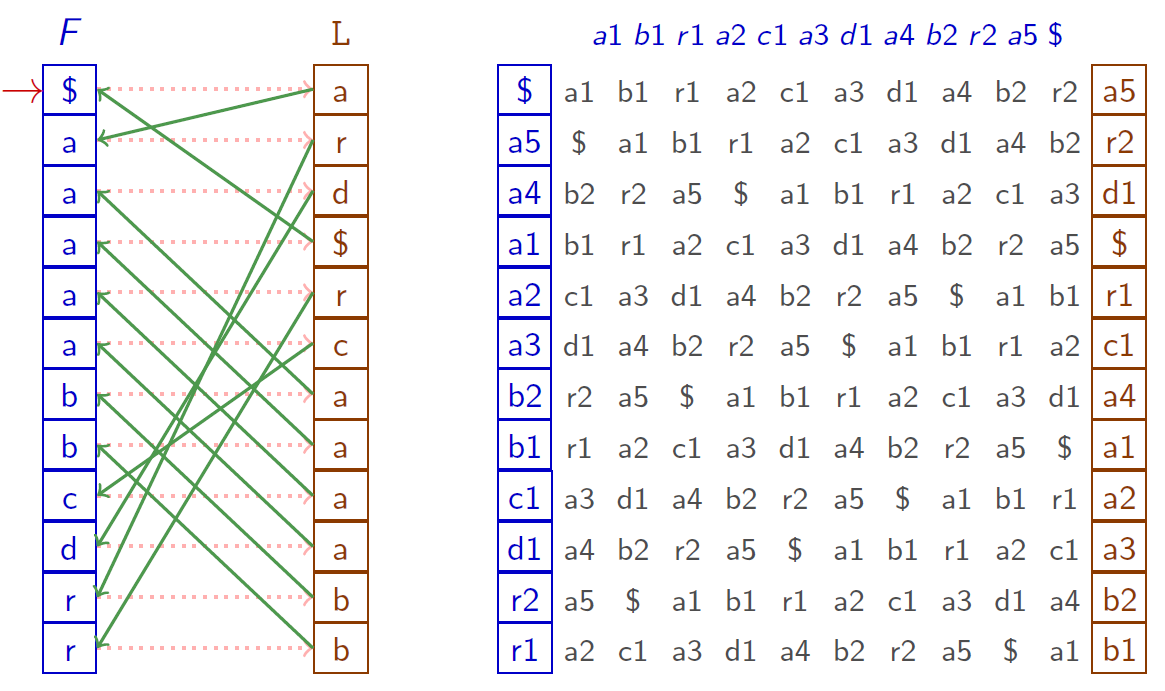
Quel que soit caractère $c$, la $i$-ème occurrence de $c$ dans $L$ et la $i$-ème occurrence de $c$ dans~$F$ correspondent au même $c$ du texteLes occurrences d'un même caractère ont le même ordre dans $F$ et dans $L$
La transformée de Burrows-Wheeler
La transformée inverse
En pratique, pour calculer la transformée inverse, on détermine la fonction $LF$ (Last to First) qui associe à chaque position $i$ de la dernière colonne $L$, la position du caractère $L[i]$ dans la première colonne $F$ (le nombre d'occurrences pris en compte).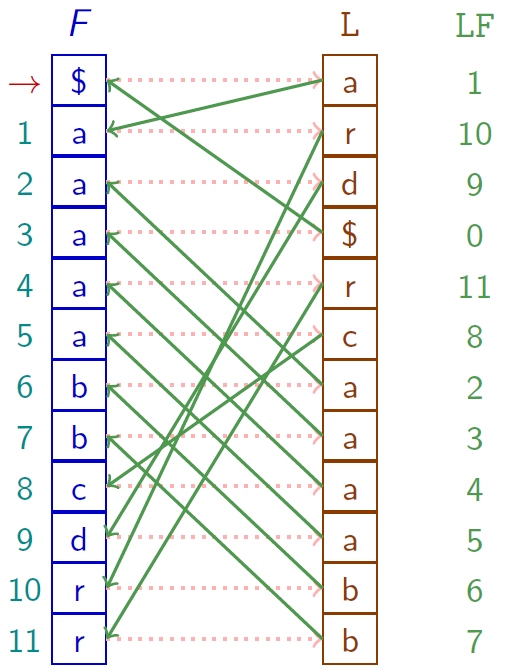
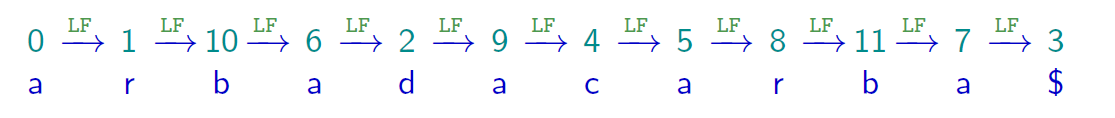
La transformée de Burrows-Wheeler
La transformée inverse
Calculer efficacement $LF$ « à la volée »

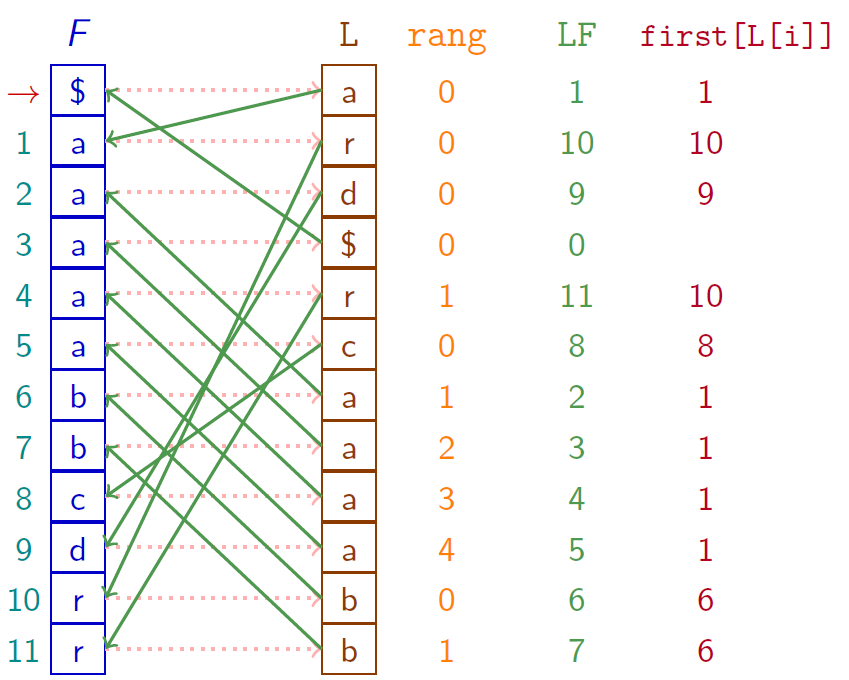
On définit
- $\text{first}[c]$ la position de la première occurrence du caractère $c$ dans $F$
- $\text{rang}[i]$ le nombre d’occurrences du caractère $L[i]$ sur les positions $< i$
On a alors $LF[i] = \text{first}[L[i]] + \text{rang}[i]$
La transformée de Burrows-Wheeler
Recherche
La recherche est guidée par la fonction $LF$ en lisant le motif à rebours (de droite à gauche, comme Frédéric Paccaut)
(À voir en séance d'exercice)
FM Index (basé sur BWT)
On parle d'auto-index, car l'index contient le texte ($\not=$ arbre des suffixes)
On veut les positions : il faut retrouver l'ordre, i.e., la table $TS$ → On échantillonne et on recalcule avec $LF$ en cas d'erreur de cache
On utilise des vecteurs de bits (librairies) pour calculer rapidement $\text{rang}$ et $LF$ (en $O(1)$ pour un alphabet de taille $o(\text{polylog}(n))$
On utilise les primitives suivantes sur un tableau de bits $B$
- accès à $B[i]$
- $\text{rank}_b(B, i)$ (nbre de bits $b$ aux positions $\lt i$)
- $\text{select}_b(B, j)$ (position de la $j$-ième occurrence de $b$